Inscription / Connexion Nouveau Sujet
Gravitation universelle
Exercice 17
1.
| Météostat | Spot | |
| Dates de lancement | 1977-1981 | 1986-1990 |
| Altitude en km | 36000 | 820 |
| Periode en min | 1440 | 101 |
| Masse en kg | 1000 | 2000 |
1.1 L'un de ces satellites est dit geostationnaire. Indiquer lequel et justifier votre réponse par le calcul
1.2 L'autre satellite est appelé satellite à défilement. Donner une explication pour ce terme.
2. Connaissant l'altitude de chacun de ces satellites, on se propose de vérifier par le calcul leur période de rotation.
2.1 Représenter le vecteur champ de gravitation terrestre en un point de l'orbite de l'un des satellites: puis établir l'expression de son intensité en fonction de ga (valeur du champ de gravitation
terrestre au sol), R (rayon de la Terre) et de h (altitude du satellite).
2.2 Par une étude dynamique, montrer que le mouvement circulaire d'un satellite terrestre évoluant à
l'altitude h est uniforme. En déduire l'expression de sa vitesse en fonction de go. R et h
2.3 Définir la période de rotation de chaque satellite, et établir son expression en fonction de go Ret h
2.4 Application numérique calculer la période du mouvement des deux satellites.
10. L'énergie potentielle de gravitation du système terre-satellite de masse m est donnée par la
relation: Ep=-mgoR²/R+h
1.1 Etablir, en fonction de m, go R et h, l'expression de l'énergie mécanique du satellite.
1.2 Le satellite SPOT est équipé d'un moteur permettant de corriger sa trajectoire.
1.2.1 Montrer que si le moteur fonctionne, toute variation ∆Em de l'énergie mécanique du satellite S'accompagne de variation simultanée ∆r de son rayon orbital et ∆V de sa vitesse.
1.2.2. En utilisant les résultats des questions précédentes, exprimer la variation de rayon orbital ∆r et la variation de vitesse ∆V corrélatives à une variation d'énergie mécanique ∆Em.
1.2.3 Calculer, pour ∆Em = 5.10^3 J, les nouvelles valeurs v' de la vitesse de Spot et r'de son rayon orbital.
Données: go=9.8ms; R=6400 km
Bonjour j'ai besoin d'aide pour les trois dernières questions de l'exo merci
1.2 Le satellite SPOT est équipé d'un moteur permettant de corriger sa trajectoire.
1.2.1 Montrer que si le moteur fonctionne, toute variation ∆Em ...
Bonjour,
En 1.1 (le deuxième !), vous avez établi Em(r). Et en 2.2 vous avez établi v(r), avec r=R+h. Donc 1.2.1 est immédiat.
Par contre 1.2.2 est plus délicat en terme de calcul au niveau Terminale : savez-vous comment calculer ∆r correspondant à ∆f avec f=A/r ?
Bonjour j'ai pas trop compris mais je ne pense pas connaître cela c'est quelle notion ? Et aussi la première question n'est pas évidente pour moi.
Pour 1.2.1 à vrai dire je ne comprends pas votre problème : si Em(r) est une fonction strictement monotone, par simple définition, le fait que Em varie "oblige" r à varier.
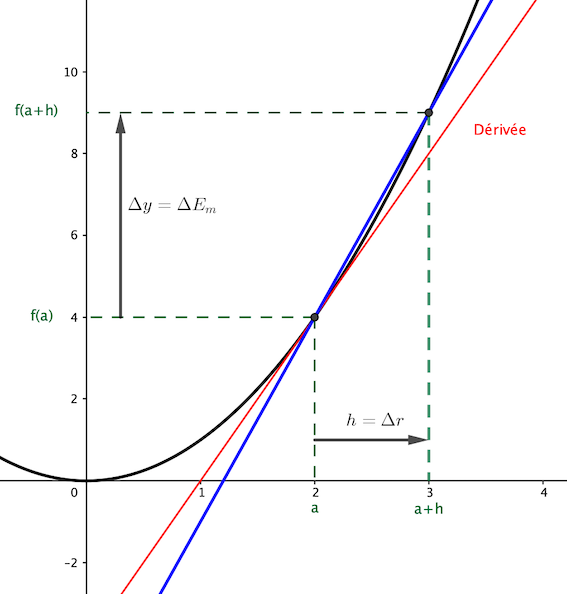
Pour 1.2.2, j'ai tracé la courbe Em(r), indiqué la variation de Em, celle de r conséquente, et en violet j'ai tracé la dérivée. On "voit" que est à peu près égal à pente de la droite violette (la dérivée).
OK je te résume ma démarche.
1.2.1 Montrer que si le moteur fonctionne, toute variation ∆Em de l'énergie mécanique du satellite S'accompagne de variation simultanée ∆r de son rayon orbital et ∆V de sa vitesse.
On a .
KMTm=CTE, .
En utilisant les résultats des questions précédentes, exprimer la variation de rayon orbital ∆r et la variation de vitesse ∆V corrélatives à une variation d'énergie mécanique ∆Em.
On a .
la dernière question je trouve r'=7276 km ,v'=65,1km/s . J'ai besoin que vous confirmiez puis je développe cette question ou si vous l'avez résolu vous me dites si on trouve la même chose, merci.
Comment arrivez vous à : ? Le
est quand même malvenu : vous écrivez
!
Rappel de l'approximation : .
Que vaut ?
Bonjour,
Non je me suis dit que lorsque Em varie donc dans son expression tout est une constante sauf le rayon r donc lorsqu'il y a une variation de l'énergie mécanique forcément ce qui va varier c'est le rayon par conséquent la vitesse aussi va varier .
Mais l'approximation dont vous me parlez jusqu'à présent je n'en ai aucune idée pour être franc lorsque vous me donniez des indices je crois que je me pert encore plus
vous n'avez pas répondu à ma question à savoir mon raisonnement est il correct.
Je voudrais savoir aussi où vous voulez en venir avec votre approximation pour m'aider à résoudre l'exercice parce que j'avoue que depuis lors qu'on on échange je n'ai pas eu plus de compréhension sur l'exercice
lorsque Em varie donc dans son expression tout est une constante sauf le rayon r donc lorsqu'il y a une variation de l'énergie mécanique forcément ce qui va varier c'est le rayon par conséquent la vitesse aussi va varier .
C'est correct pour la question 1.2.1
vous n'avez pas répondu à ma question à savoir mon raisonnement est il correct.
La phrase "Le
Je voudrais savoir aussi où vous voulez en venir avec votre approximation
La question est "exprimer la variation de rayon orbital ∆r... corrélative à une variation d'énergie mécanique ∆Em."
Je vous indique, pour la troisième fois,
Si vous calculez la dérivée, cela vous donne bien une relation entre ∆r et ∆Em, et donc répond à la question, non ?
Cette approximation, vous la connaissez et l'avez déjà utilisée : c'est la technique de calcul de la vitesse à partir d'une série de points x(t).
D'accord on avance maintenant la question 1.2.1 c'est bon .
Pour la question 1.2.2 vous avez dit que c'est incorrect donc ce que je comprends dans votre message c'est : dEm/dr ≈ ∆Em/∆r puis je derive dEm supposons que c'est= q donc dEm/dr= q ensuite je tire ∆r =∆Em/q n'est ce pas ce que vous essayez de me dire ? Puis pour ∆v je fais la même chose : dv/dr≈∆v/∆r puis je tire ∆v dans cette approximation c'est ça ?
D'accord mais avant vous pouvez me dire pourquoi cette approximation parce que je n'ai jamais vu cela et j'ai l'habitude avant d'écrire quelque chose de bien le comprendre
Vous l'avez déjà vu : calcul de la vitesse
Dit avec des mots de physicien (si un mathématicien passe par là, il corrigera)
Donc si h est "suffisamment" petit
Illustration graphique : sur laquelle on voit que la pente bleue (avec les Δ) est à peu près égale à la pente rouge (la dérivée)
J'ai compris à peu près ce que vous avez écrit mais je n'ai pas compris le rapport entre ce que vous avez écrit et l'exercice
Pourriez-vous préciser ?
Vous ne voyez pas de rapport entre quoi et quoi ?
Entre (1) et la question 1.2.2 ?
Ce ne peut être cela puisque vous avez utilisé (1) pour résoudre 1.2.2.
Donc où est précisément le problème ?
Le problème est que je ne comprends pas pourquoi dEm/dr≈∆Em/∆r même après vos explications c'est encore flou dans ma tête.
dEm/dr c'est dérivée donc la pente de la courbe au point considéré
∆Em/∆r c'est le rapport entre la variation de Em et la variation de r donc le (Em(r+h)-Em(r))/h de la définition de la dérivée et par définition de celle-ci lorsque h est petit le rapport des variations tend vers la dérivée.
Le dessin ne vous aide pas (droite bleue vs. droite rouge) ?


