Inscription / Connexion Nouveau Sujet
Grandeurs sinusoïdales
Bonjour tout le monde, aidez-moi moi ici
Question
Trois dipôles montés en série, ont à leurs bornes des tensions instantanées exprimées en volts, d'équations respectives :
;
;
Démontrer que l'expression de la tension instantanée aux bornes de l'association s'écrit :
J'ai commencé par poser que :
)
Avec
Mais ce résultat est différent de celui qui est attendu. En plus, j'ai du mal à trouver le déphasage 
.
Bonjour
Le théorème de Parceval est à ton programme ?
Revérifie quand même ton calcul.
Tu peux utiliser les vecteurs de Fresnel à moins que la méthode des grandeurs complexes associées te soit aussi connue.
Alors là, je ne comprend pas comprend faire.
J'ai pensé aux vecteurs de Fresnel.
Mais la suite...je n'ai pas pu franchement
Ok pour ta somme des vecteurs de Fresnel. Tu projetes sur deux axes comme tu le ferais avec une somme de vecteurs forces.
Désolé pour le schéma fait à main levée.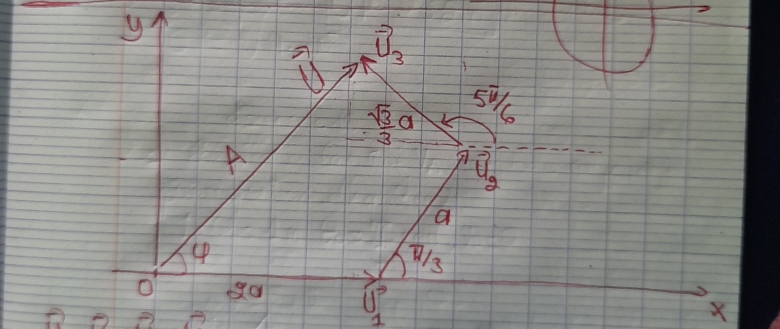 
Sur l'axe (Ox) : Ux = U1x + U2x - U3x
Acos = 2a + acos(
/3) + (
3/3)à.cos(5/6)
Alors : A.cos = (4/3)a (1)
Sur l'axe (Oy) : je fais la même chose et je trouve ceci :
Asin = a(3)/2 (2)
La construction de Fresnel est correcte dans son principe mais n'est pas à l'échelle, ce qui n'est pas grave puisque tu raisonnes sur les propriétés des sommes vectorielles. La méthode est la même qu'en mécanique. La projection de la somme vectorielle sur les deux axes conduit à :
(1)
(2)
La division membre à membre de (2) par (1) conduit à tan() puis à .
La somme membre à membre de (1) et (2) après élévation au carré conduit à A2 puis à A.
Alors : A.cos
= (4/3)a (1)
Sur l'axe (Oy) : je fais la même chose et je trouve ceci :
Asin
= a(3)/2 (2)Tu es bien sûr de toi ?
Annuler
connectez vous