Inscription / Connexion Nouveau Sujet
Forces de réaction et force normale
Bonjour, ou plutôt bonsoir ! 
Dans le cadre de mon TPE (sur les montgolfières) je suis amené à faire un bilan des forces qui s'exerce sur une montgolfière avant de la faire décoller. (C'est-à-dire que son enveloppe est gonflé d'air ambiant mais le brûleur n'est pas encore allumé).
On néglige les frottements avec l'air.
J'ai représenté la montgolfière sous forme de cube. Vous trouverez mon schéma ci-joint.
J'ai indiqué la poussée d'archimède (notée Fa ) et le poids (Fg)
[i]La limite d'image du site étant beaucoup trop petite pour la photo, je me permet exceptionnellement de mettre un lien vers l'image : 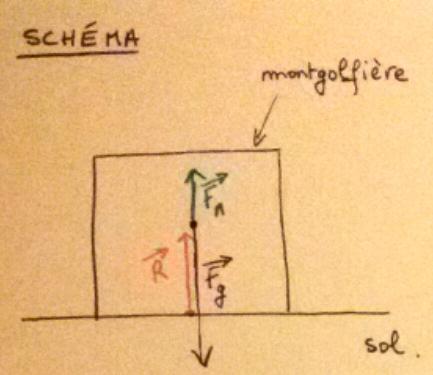
Voici mon problème :
Je ne sais pas comment calculer l'intensité de la force de réaction ni la force normale (notée R)
J'ai suivi ce raisonnement :
Je sais que le vecteur force de réaction est égal à la somme des composantes vectorielles de la force normale (perpendiculaire au sol) et de la(ou les) force(s) de frottement.
Or ici, comme on néglige les frottements, cela signifierait que le vecteur force de réaction est égal au vecteur de la force normale et est donc perpendiculaire au sol.
De plus, on sait que la montgolfière est statique (ou respecte le principe d'inertie étant donné que sa vitesse vaut 0 ). De ce fait, la somme des composantes vectorielles est égal à un vecteur nul.
Avec ce raisonnement, j'ai pu écrire cette équation (je n'ai pas réussi à écrire avec des vecteurs) :
Fa + Fg + R = 0
R = -Fa - Fg
Ce qui me permet de trouver le vecteur R.
Est-ce correct ?
Si c'est le cas, j'aimerais poser une autre question concernant le décollage :
Pendant le décollage, sous l'action de la chaleur, la masse volumique de l'air contenu dans l'enveloppe diminue. De ce fait, la masse totale de la montgolfière diminue et par conséquent son poids.
De plus,la Poussée d'Archimède ne varie pas car le volume déplacé ne change pas.
Ce que je ne comprend pas : Pendant tout ce procédé, est ce que le vecteur R diminue de manière proportionnelle à la "diminution" du vecteur Fg ?
La montgolfière décolle au moment où Fa > Fg + R ou bien seulement quand Fa > Fg ?
Je suis un peu perdu 
Merci d'avance 
***Image insérée sur le forum et recadrée***
Hello
1) Phase ou la montgolfière est sur le sol
on sait que la montgolfière est statique
Donc de fait, les frottements sont nuls! On n'a même pas à les "négliger"
Attention tout de même à l'évaluation de la force d'archimède lorsque la montgolfière est posée sur le sol. La première chose à clarifier serait il me semble: quel est le système que tu étudie: le ballon? le ballon + la nacelle? La seconde étant: le ballon est il en contact avec le sol? Ou bien flotte t il?
Ceci étant, on pourra toujours ce dire que cette phase n'a pas réellement d'intérêt, ce qui compte c'est de décoller

2) Phase de décollage
Pendant le décollage, sous l'action de la chaleur, la masse volumique de l'air contenu dans l'enveloppe diminue. De ce fait, la masse totale de la montgolfière diminue et par conséquent son poids.
Cela voudrait dire, qu'une partie de l'air (initialement froid) contenu dans l'enveloppe s'échappe lorsque l'aérostier le fait chauffer...

L'enveloppe est initialement partiellement remplie d'air froid, on fait chauffer cette masse constante d'air, donc son volume augmente, et si son volume augmente, la poussée d'archimède également ...
Un exercice qui peut t'intéresser qui a été traité sur le Forum il y a quelques jours:
Merci pour votre réponse,
1) Phase ou la montgolfière est sur le sol
\vec{R} = -\vec{F_a} - \vec{F_g} hum hum ...
Je suppose que c'est faux?
Le système étudié est (ballon + nacelle).
le ballon est il en contact avec le sol? Ou bien flotte t il?
Je vais préciser un peu l'objectif de mon TPE, histoire d'être le plus précis possible.
Je cherche à déterminer la Température nécessaire au sein de l'enveloppe pour que celle-ci décolle.
Afin de simplifier les choses, j'avais représenté le ballon et la nacelle dans un même axe perpendiculaire au sol (et pour ne pas s'encombrer avec le centre de carène...).
Un peu comme ceci : https://youtu.be/__iAh-M8Hb0?t=5m33s
Concernant le ballon : dans la réalité, lorsque l'on chauffe l'air, le ballon encore en contact avec le sol, de même que la nacelle. Je sais que c'est faux de dire que le ballon flotte déjà dans l'air (= car il a déjà été redressé par de l'air chaud) mais dans mes calculs j'ai considéré que l'air était froid.
Or avec l'oubli de la force de réaction, je crains que tout ne soit faussé !! Etant donné que j'ai cherché la température seulement pour que P. Archimède > Poids.
D'où je vous réponds par une question
 : la force de réaction joue-t-elle un role important dans ce que j'étudie ?
: la force de réaction joue-t-elle un role important dans ce que j'étudie ?
2) Phase de décollage
Merci, grâce à vous, je m'en rend compte que le ballon n'est pas effectivement rempli entièrement rempli d'air froid

De plus l'exercice va m'être très utile ! J'ai l'impression que la force de réaction n'est pas prise en compte ici, en tout cas dans cet exercice.
Je vais retravailler ça en attendant votre réponse.
La réaction du sol est sans intérêt dans ton étude (il me semble)
Cette réaction est encore non nulle (ie la nacelle est posée sur le sol ) alors que le ballon "flotte" déjà dans l'air. Ce qui t'intéresse c'est l'étude comparative de :
- la poussée d'archimède
- le poids ballon équipé + air chaud
D'accord, merci pour vos éclaircissements.
Donc si j'ai bien compris, la poussée d'archimède ne changera plus seulement quand l'enveloppe de la montgolfière est entièrement rempli. Et par la suite, si la température augmente encore, les molécules d'air s'échappent de l'ouverture, ce qui provoque une diminution du poids?
J'ai fait l'exercice que vous m'avez montré. Toutefois, je ne comprends pas pourquoi il est nécessaire que la montgolfière ne soit pas entièrement remplie d'air froid 
Par ailleurs, j'ai exprimé la température tel que Pa = P (fichier joint).
Avec :
M la masse molaire de l'air (0.0288 kg/mol)
P la pression en Pa (ici 101 325)
T_amb la température en Kelvin
Va = V_enveloppe*3/4 (en m^3)
R la constante des gaz parfaits (8,314 462)
Je n'y arrive seulement quand V1 < V ... Après, je ne sais pas comment faire :/
Désolé de vous embêter, je sais que ça n'étais pas le sujet d'origine 

Dans la pratique:
par des ventilateurs on met de l'air dans l'envelopper (l'enveloppe reste au contact du sol)
à un certain moment (enveloppe partiellement remplie d'air froid) on commence à chauffer l'air contenu dans l'enveloppe et on arrête la ventilation:
on peut modéliser cette phase par: quantité d'air dans le ballon est constante (masse air constante), mais avec la température son volume augmente, la force d'archimède également et donc le ballon s'élève
A masse constante, on atteint le volume maximal de l'enveloppe. Si on continue à faire chauffer l'air contenu, celui ci n'aura d'autre solution que de s'échapper du ballon
Donc à volume constant la masse diminuera, tandis que la force d'archimede reste constante (le volume d'air froid déplacé est le même). Le ballon continue de monter.
On arrête le chauffage. L'air dans l'enveloppe refroidit, son volume également, la force d'archimède diminue, le ballon descend.
Est ce plus clair formulé ainsi?


