Inscription / Connexion Nouveau Sujet
Forces.
Bonjour, j'ai un exercice à faire avec le principe de l'inertie de 1ère mais je ne l'ai pas bien compris..
Si vous pouviez m'aider !
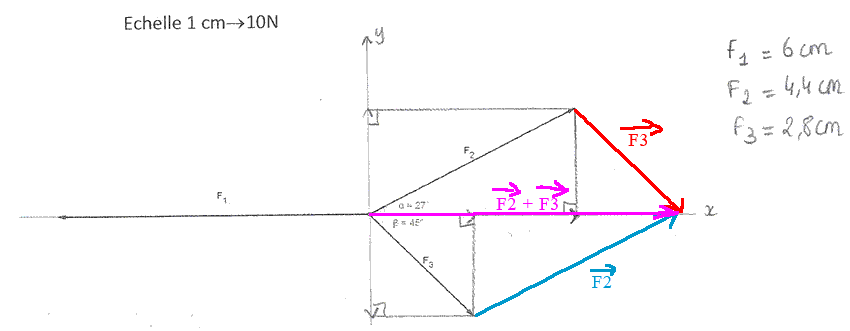
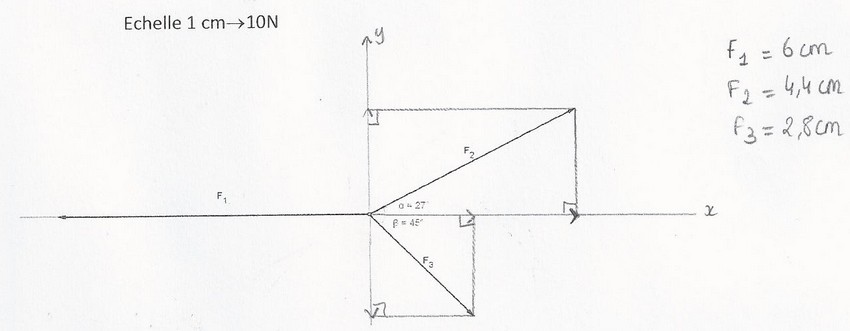
On considère un anneau de masse négligeable en équilibre, soumis à la tension de trois dynamomètres.
1. Appliquer le principe de l'inertie.
2. Par une méthode géométrique, montrer qu'il est respecté.
3. Mesurer puis projeter les trois forces et établir la condition d'équilibre.
Merci d'avance pour votre aide.
Bonsoir.
1) Principe d'inertie
Rappelez-vous ce que dit le principe d'inertie !
Si un objet n'est soumis à aucune force (ou à des forces se compensant), alors soit il est au repos, soit il est animé d'un mouvement rectiligne uniforme.
Donc appliqué ici, vous avez :
2) Relation de Chasles (méthode géométrique).
Pour prouver le principe d'inertie... On utilise la relation d'addition des vecteurs, à savoir la relation de Chasles...
(*) Soit vous ajouter "bout à bout" les vecteurs-forces.
(*) Soit, par la règle du parallélogramme, vous tracez la somme de et de
puis vous montrer qu'il est bien l'opposé de
- au choix !-
3) Projections
Comme vous l'avez bien fait sur votre schéma, vous avez projetez vos forces.
Ainsi, vous constatez que les résultantes des forces projetées s'annulent 2 à 2, à savoir :
(*) F2y compense F3y (ils ont la même longueur mais des sens opposés)
(*) F1x compense F2x + F3x
La condition d'équilibre s'écrit donc :
(*) F2y = F3y
(*) F1x = F2x + F3x
Ou autrement dit, en faisant intervenir les angles :
(*) Sur (Ox) : -F1 + F2.cos(
) + F3.cos(
) = 0
(*) Sur (Oy) : 0 + F2.sin() - F3.sin() = 0
Joyeux Noël !
J'ai une autre question :
Soit, par la règle du parallélogramme, vous tracez la somme des vecteurs F2 et de F3 puis vous montrer qu'il est bien l'opposé de F1
Je ne sais pas comment faire pour le montrer..
En utilisant 
v(G) = 0, ça signifie que votre mobile est en MRU ou au repos, donc que la somme vectorielle de vos forces est nulle, ce qui représente votre exercice en terme d'équilibre...
Donc ça ne change rien !
Je ne sais pas comment faire pour le montrer..
En mesurant F2 + F3 et en constatant que c'est la même longueur que F1 (mais des vecteurs opposés !)
Comme ça :
Annuler
connectez vous