oups désolé pour les fautes de frappe...

Bonjour,

1) Les deux forces sont :
. le poids
. la réaction de la piste (somme de la réaction normale - ou perpendiculaire - à la piste et des forces de frottement opposées au déplacement donc orientéees vers le bas de la piste puisque le surfeur remonte la piste)

2) oui, on connaît complètement le poids
Attention : n'écris pas que la direction est "la verticale de la piste" ; écris simplement que la direction du poids est la verticale.

3) la piste à 45° par rapport à l'horizontale
un point O sur cette piste
le poids : un vecteur le représente, tu as toutes les informations
la réaction de la piste : un vecteur orienté à 30° de la perpendiculaire à la piste et vers le bas. La question est "quelle est l'intensité de cette réaction ?", mais tu n'as pas posté tout ton énoncé.

super; oui en éalité pour la 1) j'ai écrit la Terre mais cela représente bien le poids.
question: pour la réaction de la piste, doit-on considérer qu'il y a des frottements ou non? car si il y en a pas, nous pouvons en conclure que la réaction est perpendiclire à la piste...
pour la 3, il y a quelque chose que je ne comprend as: j'ai un petit dessin sur mon cahier ui représente la situation et apparemen la réaction de la piste est vers le HAUT. j'ai ma petite idée: s'il y a des frottements on a R= Rn +Rt avec Rn perpendiculaire à la piste et Rt qui vas vers le bas...

Question sur les frottements :

Citation :
L'action de la piste sur système est équivalente à une force R de point d'application I. La direction de ce vecteur fait un angle = 30° avec la perpendiculaire à la piste.

ok ok^^ désolé de ne venir que maintenant: je suis en pleine préparations pour ce soir. je reviendrai demain pour continuer cet exercice! désolée....bonne fêtes!!

je vais essayer de réaliser un montage pour vous l'envoyez. j'ai l'impression que O est confondue avec I?

Oui, tu peux confondre les points O et I

super^^ bon je me mets au boulot, et je vous envoie ça tout de suite.

je précise néanmoins, la suite de l'énoncé:
les vecteurs forces seront représentés sur le schéma avec la même origine O et à l'échelle 2.0 cm(==)100N
4)représenter le vecteur poids
5)en deduire graphiquement et sans justification le vecteur Rn.
6)Connaissant Rn et l'angle B, représenter R. DEterminer à partir du graphe son intensité.
7) en déduire graphiquement Rt, donner ses caractéristiques
8)quelle est la valeur de la force de frottement f de la piste sur le surf?
9)comment se peut-il que le surfeur remonte la piste?

aprés avoir répondu à ces question j'attaquerai la troisieme et derniere partie de cet exo.

voici le dessin:

ooops je me rend compte qu'il ne fallait pas représenter le sol...

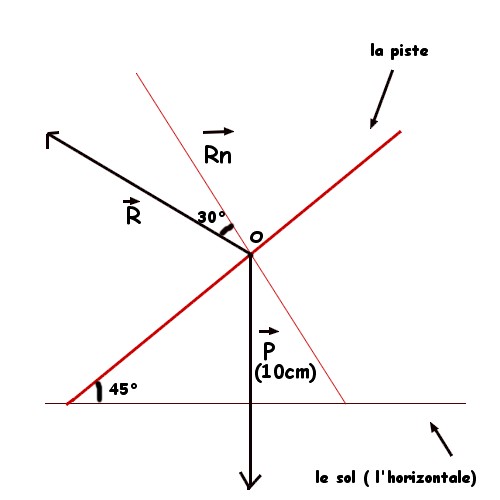
Ce n'est pas gênant d'avoir représenté le sol.



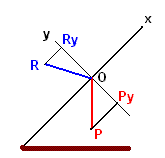
Il monte la pente. Il est probable qu'il ralentit et que le vecteur variation de vitesse (accélération) est parallèle à cette pente. D'après la deuxième loi de Newton la résultante (somme vectorielle) des forces est donc parallèle à la pente.

En conséquence si cette somme vectorielle des forces est projetée sur un axe perpendiculaire à la pente (y'Oy) la somme des projections (la somme des composantes sur cet axe) est également nulle.
Sur mon dessin (qui n'est pas à l'échelle et ne respecte pas les angles) j'ai fait figurer les projections du poids et de la réaction de la piste sur cet axe perpendiculaire à la pente : ce sont les composantes P_y et R_y
Que vaut P_y ?
Que vaut en conséquence R_y ?
Et donc que vaut R ?

mais je n'ai pas encore vu en cours la 2nde loi de newton...
ps: mon schéma était faux?

Ton schéma non seulement n'était pas faux, mais il est même très bien, et à l'échelle.
Le mien donne quelques indications de plus pour la suite de l'exercice

Tu n'as pas encore vu la seconde loi de Newton : alors tu n'as besoin de savoir qu'une seule chose :

La somme est un vecteur parallèle à la piste, donc parallèle à x'Ox

ok et cette information est censé m'aider pour les pochaines quesions?
car pour la 5, je vois à peut pret à quoi ressemble Rn: il sagit de la perpendiculaire à la piste? mais il me faut connaitre son intensité?

Oui, R_n est ce que j'ai noté R_y sur ma figure.

Oui, tu peux calculer R_n (mon message de 13 h 30 et celui de 16 h 22)

ok ok, bon ben pour Rn, si je veux son intensité il me faut sa mesure en cm, or je ne l'ai pas?? par contre je sais qu'il y a un angle de 90° entre Rn et la piste , je dois m'aider de ça?

Non, tu dois t'aider de ce que la somme est parallèle à la piste donc à l'axe x'Ox

"En clair", cela signifie que |R_n| = |P_y|

Les projections de et de sur l'axe perpendiculaire à la piste ont même valeur absolue. Ainsi la somme de ces deux composantes sera nulle.

ok mais avant pourriez vous m'expliquer pourquoi P +R est parallèle à la piste ?

je viens de faire rapidement la somme des deux vecteurs (c'est censé etre un parallélogramme) sur mon dessin et voila ce que j'obtiens (en vert).

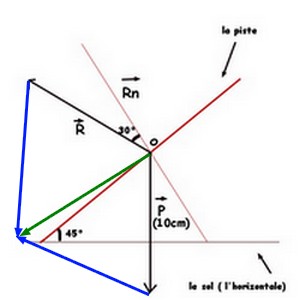
Sur ce dessin de 17 h 12, la valeur de n'est pas correcte... puisque la résultante n'est pas parallèle à la piste !

Construction :
.
. puis de l'extrêmité du vecteur une parallèle au vecteur et l'intersection de cette parallèle avec la piste : ceci donne la valeur correcte de

Si la résultante des forces n'était pas parallèle à la piste le surfeur ou bien décollerait ou bien s'enfoncerait dans la piste.
La résultante des forces est parallèle au vecteur "variation de vitesse" - ceci est la deuxième loi de Newton - . Comme la vitesse est à tout instant parallèle à la piste la "variation de vitesse" ne peut être qu'elle aussi parallèle à la piste.

ah ok c'est bon je viens de comprendre.
serait-ce possible que vous m'illustriez cela sur votre schéma de 13h30? je pourrai alors trouver la réponse à la question 5.

Tu devrais suivre ton énoncé qui est très précis :
4) Le vecteur poids
5) Projection du vecteur poids sur la perpendiculaire à la piste (ce que j'ai nommé P_y sur mon dessin)
R_n est strictement égal et opposé à P_y, donc très facile à construire
6) R_n est la projection du vecteur R sur la perpendiculaire à la piste ; connaissant R_n alors R devient lui aussi très facile à construire puisque l'angle est connu.
7) C'est seulement ensuite que l'on projette R sur l'axe parallèle à la piste pour trouver R_t

Une figure (il faudrait mettre des vecteurs !)



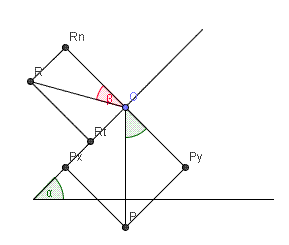
Le poids est décomposé en P_x et P_y
P_y est égal et opposé à R_n
R_n permet de connaître l'intensité de
est projeté en R_t, d'où l'intensité des forces de frottement.

ah daccord, merci pour le schéma.

les deux angles en vert sont donc égaux?  car si c'est le cas on peut alors determiner Py sachant que P=500N et que POPy=45°
cos45°= Py/500 d'où Py= cos45° * 500
et sachant que /Py/=/Rn/ on peut determiner Rn (son intensité)

puis avec Rn comme vous l'avez vous même dit, on peut trouver R en s'aidant de l'angle B.

?

Bien sûr que les angles en vert sont égaux (deux angles aux côtés perpendiculaires deux à deux sont égaux : la perpendiculaire à la piste est ... perpendiculaire à la piste et la verticale est perpendiculaire à l'horizontale).

Si j'ai bien compris on ne te demande justement pas les calculs avec la trigonométrie. On te demande un dessin à grande échelle et des mesures de longueurs sur ce dessin (puisque tu sais le faire tu peux toujours vérifier par le calcul trigonométrique )

ok en gros je m'aide du dessin^^pas la peine de s'envoler dans les calculs.
pour la 6) vous avez raison , R est trés facile à construire. pour son intensité, j'a utilisé la trigonométrie: sur mon graphe (angles respectés) Rn =Py=11.5cm (soit 575N) grace a la trigo, je trouve que R=10cm soit 500N. c'est a peu prés la meme intensité que P , est ce nomal?

Les valeurs de forces ou de composantes que tu annonces ne sont pas correctes.

R_n et P_y ont une intensité inférieure à celle de P, donc inférieure à 500 N

j'ai refais mes calculs: je trouve Rn=Py=7cm soit 350N, et là?

Oui, là ça va très bien !

(par le calcul P_y = R_n = P * cos(45°) = 500 * (2) / 2 354 N

ok ben c'estsuper! finalement les calculs nous permettent de trouver la mesure et d'en déduire l'intensité...bon ben ça change tout pour R alors:
a propos maintenant on connais Rn et on a l'angle B , on peut utiliser la trigo mais comment savoir entre Rn et R lequel est l'hypothénuse?

Rn est la composante de sur l'axe Oy

Le point Rn sur le dessin est donc obtenu en projetant orthogonalement l'extrêmité du vecteur sur l'axe Oy

Quel est donc l'hypoténuse dans ce triangle rectangle ?

je dirais R... puis Rn+Rt "forment" R donc Rn est logiquement plus "petit" que R

enfin voila c'est ce que je pense...

a non!

oops , non c'est rien désolé

Oui c'est qui est l'hypoténuse !

^^ bon j'ai fais mon calcul, R est de 6 cm a peu prés soit 307N

L'intensité de R est supérieure à R_n qui vaut environ 354 N

attendez Rn=354N
cos30°=7/R soir R=7/cos30=8cm; oops j'ai multiplié je crois^^ donc ce qui équivale à 400N

le pire dans tout ça c'est que c'est logique! R ne peut pas etre inférieur a Rn ni a Rt dailleurs

pour etre plus précise je pense que ça serait même 409N

Très bien !

R = 500 * cos(45°) / cos(30°) 408 N

Mais respecte bien ton énoncé :

Citation :
6) Connaissant Rn et l'angle , représenter R. Déterminer à partir du graphe son intensité.

mais en fait on est bien obligé à un moment donné de faire un petit calcul non? au moins pour trouver la mesure . ensuite grace à l'échelle et au graphe on détermine son intensité?

Non, jusqu'à maintenant il n'y a besoin d'aucun calcul.

Le point O ; à l'échelle, le vecteur il est vertical vers le bas ; de son extrêmité la projection sur y'Oy ; d'où la mesure de l'intensité de P_y ; par symétrie par rapport au point O, la construction de R_n de même intensité que P_y ; la perpendiculaire à y'Oy intersecte le support de R incliné de 30° vers l'arrière : d'où le point R et donc la mesure de l'intensité de R ; la projection du point R sur l'axe x'Ox d'où le point R_t et la mesure de l'intensité de R_t

Tout se fait graphiquement ; il n'y a eu aucun calcul.

oui daccord , mais atendez (je veux bien comprende désolé^^)
par ex pour Py, je suis daccord avc vous quand vous me dites qu'elle a été projeté: c'est assez facile à tracer mais comment savoir si cette force mesure 6 , 7, 8 cm? il a bien fallu s'aider de l'angle pour determiner cela?

Bien sûr, mais l'angle c'est du dessin, c'est une construction géométrique ( = 45° et = 30° cela se construit géométriquement). Ensuite ayant donné la longueur 10 cm pour 500 N au vecteur il suffit de mesurer avec un double-décimètre les longueurs de P_y et de R pour trouver qu'elles valent environ 7 cm et environ 8 cm et donc que les intensités correspondantes sont voisines de 350 N et de 400 N
Il n'y a pas de calcul, pas d'emploi de la trigonométrie.

ahhh ok je crois que je comprends! on aurai pu aussi utiliser une équerre et on aurai alors pu voir approximativement la mesure de Py...?

ok revenons à la question 7) j'ai ma petite idée , en fait j'en ai même deux mais je ne suis pas encore sure:
puisque R=Rn+Rt  on a 8cm=7cm+Rt d'ou Rt=1cm=50N
ou encore R=Rn+Rt d'ou 408N=354+RT d'ou Rt=54N

graphiquement Rt est tangente au point de contact entre le surfeur et la piste. son sens: vers le bas(opposé au glissement du surfeur qui ici est vers le haut)
la valeur de la force de frottement, donc Rt= 50/54N

Ce ne sont pas des sommes de scalaires (7 + 1 = 8) ce sont des sommes de vecteurs

Pour connaître la valeur de R_t il faut prendre son double-décimètre et mesurer soigneusement sur le dessin. Puis convertir avec l'échelle.

^^ je me disais aussi: en mesurant je trouve 3.5cm. soit 175N

Je pense que la longueur sur le dessin vaut plutôt 4 cm ce qui correspond à environ 200 N

Vérifications : pour se rassurer ! pas pour faire le problème qui se fait graphiquement :
. ou bien R_t R * sin(30°) = (1/2) * R 408 / 2 = 204 N
. ou bien R_t = P * cos(45°) * tan(30°) = 500 * [(2) / 2] * [(3) / 3] = 500 * (6) / 6 204 N