Inscription / Connexion Nouveau Sujet
Force électrostatique/Champ électrique
Bonjour !
Je chercherais une explication en ce qui concerne cet exercice... c'est un QCM de physique et je suis certaine d'oublier une propriété toute bête sur les vecteurs mais bon je sèche un peu (mes connaissances du lycée se sont dissipées x)).
Voici l'énoncé:
On considère un triangle ABC dont les longueurs AC et BC valent respectivement 10 pm et 5 pm, et l'angle C=120° . On place en A une charge qA=4.10^-10 C et en B une charge qB=10^-10 C. Quelle est la valeur du champ électrique créé au point C par ces deux charges ?
Alors il me semble qu'il y a deux solutions: en représentant la situation on peut se rendre compte que le vecteur E final est a bissectrice des vecteurs EA et EB car ces deux derniers sont de longueurs identiques (EB=k*(qB/r²B)=k*(qA/4)/(r²A/4)=k*qA/r²A=EA) ainsi en utilisant cos 6O°= (Ef/2)/EB on peut trouver EB : avec cette méthode je trouve bien la réponse qui est 3,6;10^22 V/m. (j'écris ce raisonnement pour éviter qu'on me réponde avec )
Cependant c'est la version plus simple que je ne comprends pas.... Il me semble que le champ électrique total qui s'exerce en un point, ici C, est la somme des champs électriques qui s'exercent en ce point donc EA+EB. Et ici EB=EA mais EA s'exerce quand même 2 fois non ? donc (dans mon raisonnement qui n'est pas le bon) E final serait 2*EA d'où 5,2.10^22 (qui est aussi une réponse du QCM).... enfin voilà je ne comprends pas pourquoi on considère que le champ électrique ici est uniquement égal à EA malgré EB....
Je vous remercie d'avance j'espère avoir été claire... 
Je ne suis plus au lycée, c'est du programme de PACES mais il me semble qu'on l'étudie terminal... et que la réponse doit être une simple propriété oubliée x)) donc je le mets section lycée.
Bonjour,
Ton énoncé décrit la situation suivante :
qA = 4 . 10-10 C et qB = 10 . 10-10 C
donc qA < qB
AC = 10pm et BC = 5pm
donc AC² > BC²
Dans ces conditions qA/(AC)² < qB/(BC)² donc EA < EB
Contrairement à ce que tu écris les modules des deux champs ne sont pas égaux.
Non.
Ne tiens pas compte de ce que j'ai écrit.
Désolé, j'ai mal lu la valeur de qB qui est de 1.10-10C et non de 10.10-10C
Il me semble que dans ta 2e version tu confondes la somme de deux vecteurs avec la somme des modules de deux vecteurs.
mais
E  EA + EB
EA + EB
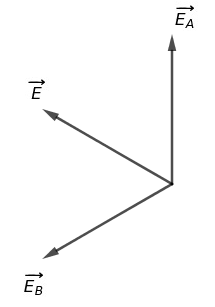
Ici, on est dans un cas particulier ou E = EA = EB
Bonjour!
Avec la représentation que tu as faite je viens juste de comprendre x) j'avais du mal à me représenter la situation où Ef=EA=EB (et oui j'ai confondu la somme de deux vecteurs et modules...).
Je te remercie pour ta réponse 
Un de mes professeurs de physique me disait ( il y a déjà pas mal d'années  )
)
" Un schéma bien fait, c'est la moitié du travail envolé "


