Inscription / Connexion Nouveau Sujet
Force de Laplace
Bonjour...
Énoncée :
Un conducteur OB de longueur l',de masse m parcouru par un courant d intensité I et plongeant dans un champ magnétique uniforme B de largeur d, est incliné a l équilibre d un angle a sur la verticale du point de suspension O.
1/exprimer littéralement
a/ la longueur l' du conducteur situé dans le champ B en fonction de d et a
b/ la force de Laplace en fonction de I,d,B et a
C/ la distance OA en fonction de L et a
2/ par application du théorèmes des moments, montrer que l équation d équilibre s écrit
Sin ^3a-sina+k=0
3/ vérifier que pour
l'=1 m, m=8 g,i=2A, L=0,75 m, d=5 cm ,B=0,1T et g=9,8 N/kg ,la valeur de a=11,,5°
Est une solution de l équation précédente.
L axe (?) est l axe de rotation de la tige et passe par le point O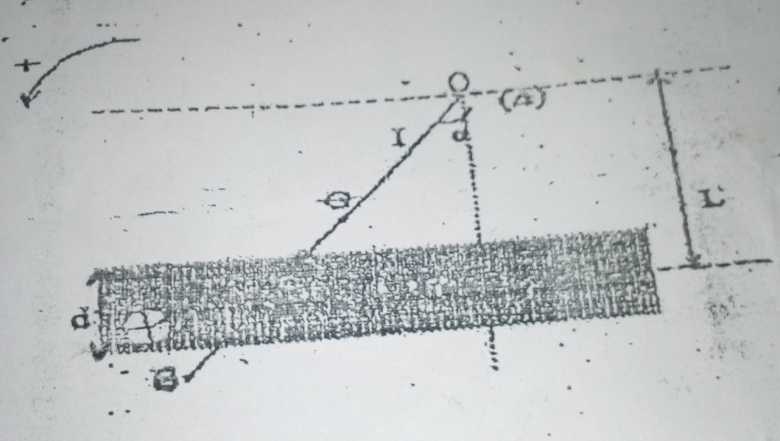
***Titre changé***
Question 1a
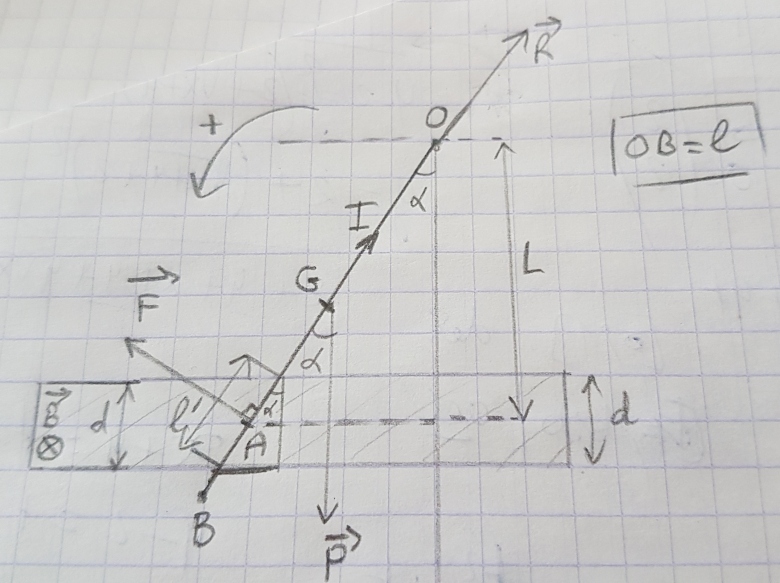
Soit OBB' est un triangle rectangle en B'
Cos a=OB'/l'
l'=OB'/cos a
Mais je ne trouve pas le d dans mon expression
Bonjour à tous,
Il faut faire un dessin, moussolony.
dautre part , si je comprends bien l'enonce qui est loin detre clair,
OB=l=1m et non pas l'
Et l' = d / cos 
Cf dessin
Question 1b
F=i*l'*B
F=i*d/cosa*B
Question 1c
OA=L/cos a
Question 2
M(P)+M(F)+M(R)=0
Comment retrouver cette équation
Sin^3a-sina+k=0
M(P)+M(F)+M(R)=0
Il faudrait préciser par rapport à quel point tu calcules les moments
P*d-F*d'=0
d=(2L*sina)/cos a et d'=sina*L/cos a
P*(2L*sina)/cosa-F*(sinaL)/cos a
Qu 'appelles-tu d, d'?
(d est déjà utilisé donc il faut eviter de le réutiliser pour autre chose)
d et d' désignent les distances par rapport a l axe (∆)
Les distances entre quoi et quoi?
Tu es trop imprecis.
Tu cherches le moment des forces par rapport à O si jai bien deviné.
Pour F appliquee en A, que vaut le bras de levier?
Idem pour P appliquee en G ?
Et pour R ?
F applique en A son bras de levier est:
OH désigné son bras de levier
Sin a=(OH)/OA et OA=L/cos a
OH=sin a*OA
OH=tan a*L
M(F)=F*tana*L
P applique en G
GH désigné son bras de levier
Sin a=GH/GO et GO=OA/2
GH=sin a *OA/2
GH=sin a*2L/cosa
GH=tan a*2L
M(P)=P*tan a *2L
F applique en A son bras de levier est:
OH désigné son bras de levier
Qu'appelles -tu H?
Mais dapres ton resultat, cest pas ca.
GO=OA/2
Non, G est le milieu de la tige, donc le milieu de ...
J'ai donc refait un dessin en precisant les points H et J pour que l'on se comprenne enfin.
(c'est à toi de faire ca! )
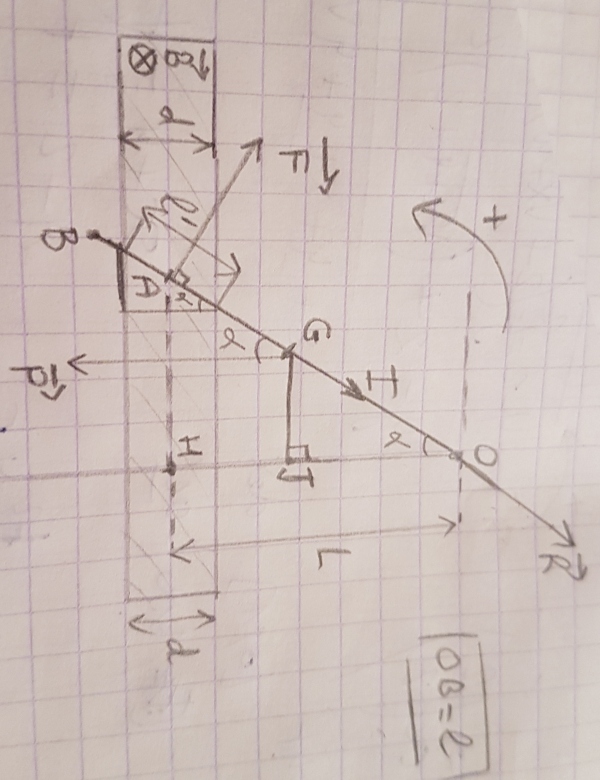
M(P)/O=mg l sin
 /2
/2Oui
Pour F, le bras de levier n'est pas AH
La force est normale à OA , c'est le cas le plus simple, donc le bras de levier est ...
Oui, il va falloir faire un peu attention aux calculs.
mg*l sin  /2 - iLBd/cos2
/2 - iLBd/cos2  = 0
= 0
mg*l sin  /2 = iLBd/cos2
/2 = iLBd/cos2 
sin  = K / cos2
= K / cos2  avec K= 2iLBd/(mgl)
avec K= 2iLBd/(mgl)
C'est presque fini...



