Inscription / Connexion Nouveau Sujet
Focométrie
 GertrudeParis
GertrudeParisBonjour
Voici l'exo:
On considère une lentille L3, de distance focale f'3 inconnue, ainsi qu'un objet réel AB.
1- A quelle condition mathématique A'B', l'image de AB par la lentille L3 , sera une image réelle ?
Justifiez votre réponse par un raisonnement mathématique.
Un expérimentateur place maintenant la lentille à une distance α de l'objet AB, telle que α soit algébriquement
égale à OA. L'image A'B' se forme à une distance β de la lentille telle que β soit algébriquement égale à OA'.
2- En posant la longueur AA' algébriquement égale à Γ (ceci est un gamma majuscule), exprimez Γ en fonction de α et β.
3- En utilisant la relation de conjugaison, ainsi que votre réponse à la question précédente, démontrez que :
𝜶𝟐 + 𝜶𝚪 + 𝚪𝒇′𝟑 = 𝟎
4- A quelle condition sur Γ ce polynôme du second degré admet-il au moins une solution réelle ?
5- En utilisant la réponse à la question précédente, déterminez l'expression des positions α1 et α2 de la lentille permettant la conjugaison de l'objet AB avec son image A'B'. Déduisez-en l'expression de γ, la distance entre les deux positions α1 et α2, en gardant à l'esprit que cette distance γ est positive.
6- En utilisant la réponse à la question précédente, démontrez que l'expression de la distance focale f'3 peut s'écrire comme :
𝑓′3 = Γ2 − 𝛾2 / 4Γ
7- En reprenant le raisonnement développé à la question 4, à quelle condition sur Γ ce polynôme du second degré admet-il une seule solution réelle ? Déterminez l'expression de cette seule position de la lentille, et déduisez-en l'expression de la distance focale f'3 dans ce cas.
Merci d'avance
Bonjour GertrudeParis
Prends l'habitude dès l'ouverture de ton sujet d'ajouter ce que tu as déjà cherché, fait, et ce qui te pose problème
Merci
Bonjour,
Je ne comprends pas la question 1, ce qui m'empêche d'avancer
Si quelqu'un pourrait bien me la reformuler et m'aider svp.
Il me semble que travailler cette fiche pourrait t'aider à faire des propositions
![]() Image formée par une lentille mince convergente
Image formée par une lentille mince convergente
Bonjour
Tu peux commencer par un schéma représentant l'image A'B' d'un objet réel AB dans les deux cas suivants :
1° : A situé entre le plan focal objet et la lentille
2° : A situé à gauche du foyer objet F.
Cela te donnera une bonne idée du résultat à chercher. L'étude mathématique est alors simple à comprendre.
Le premier schéma manque d'intérêt ici. Les 2 autres correspondent à la question. Tu peux les commenter, histoire de montrer que tu comprends quelque chose à l'optique...
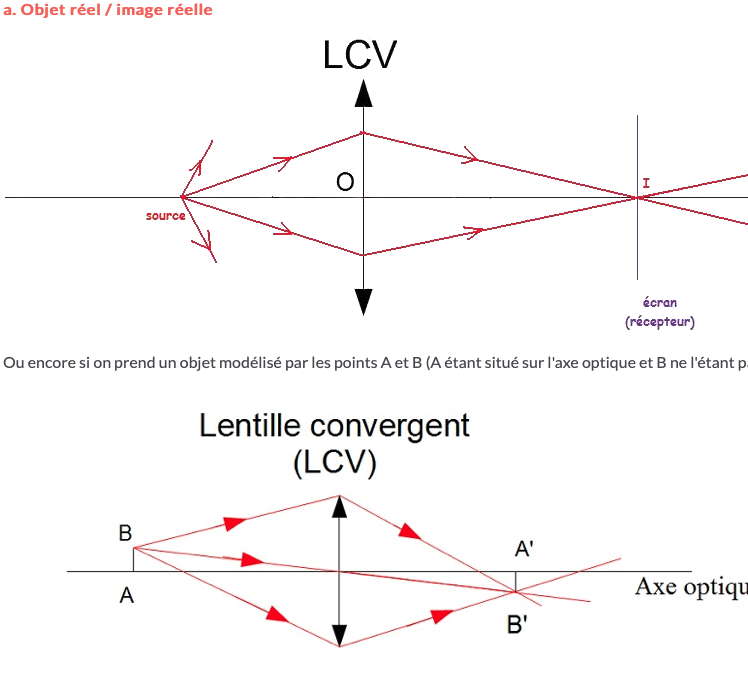
Pour la première c'est une image réelle car tous les rayons qui lui parviennent sont réels (elle peut être recueillie sur un récepteur).
Une image réelle est située à droite de la lentille.
Par contre pour la deuxième tous les rayons lui parvient mais elle n'est pas située à droite de la lentille.
Toujours pour la deuxième image, le point B' est à l'intersection des prolongements des rayons émergents.
Oui mais les positions des foyers F et F' ne sont pas précisés sur le schéma, ce qui en réduit considérablement l'intérêt.
Le schéma ici en haut à droite est plus intéressant : ![]()
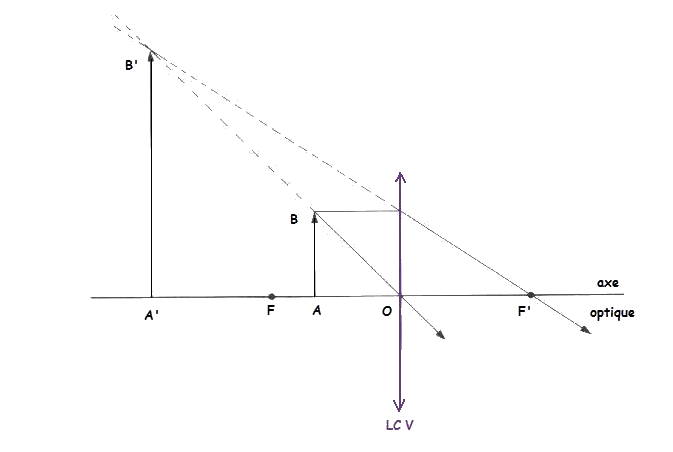
En revanche, le dernier schéma que tu fournis est très intéressant.
J'espère que tu pourras maintenant répondre à la question 1 : d'abord en regardant les schémas pour bien comprendre, ensuite par le calcul comme demandé par l'énoncé.
Dans le premier cas , OA' > 0, c'est pour cela que l'image est réelle
Dans le second cas, OA' < 0, c'est donc une image virtuelle.
Exact mais il y a une autre différence très importante : dans un cas l'image est réelle, dans l'autre cas elle est virtuelle. Tu as bien compris la différence entre ces deux cas ?
Ah,
Dans l'image virtuelle, il n'y que par F' que le rayon passe.
Alors quand l'image réelle, des rayons passe par F', mais aussi par F
Il y a aussi la taille des objets et images
Au-delà de la distance focale l'objet donnera une image réelle.
Histoire de voir si tu as compris :
1° : tu pourrais rappeler les définitions de "réel" et virtuel" pour un objet ou une image en optique ?
2° : tu pourrais donner une utilisation pratique simple d'une lentille dans le cas de la figure 2 (image réelle) et dans le cas de la figure 3 (image virtuelle) ?
Finalement : à quelle condition l'image est-elle réelle ?
1° On appelle objet le point d'intersection des rayons incidents au système optique.
-Celui-ci est réel si tous les rayons qui lui parviennent sont réels. Un objet réel est situé à gauche de la lentille.
-Un objet est virtuel si au moins un des rayons qui lui parviennent est virtuel et il est situé à droite de la lentille.
L'image d'un objet par une lentille est l'intersection des rayons qui parviennent sur le système optique.
- Une image est réelle si tous les rayons qui lui parviennent sont réels Une image réelle est située à droite de la lentille.
-Une image est virtuelle si au moins un des rayons qui lui parviennent est virtuel.
Une image virtuelle est située à gauche de la lentille.
2° figure 2 (image réelle): utilisation dans appareils photo
figure 3 (virtuelle): plutôt dans les loupes
Dans le cas d'une image réelle, A est à gauche de F
Dans le cas d'une image virtuelle, A est à droite de F.
C'est cela.
Tu dois donc démontrer, à partir de la formule de conjugaison de Descartes :
image réelle soit si
image virtuelle soit si
La relation de conjonction de Descartes s'écrit : 1/OA' - 1/OA = 1/OF'
Distance objet :
OA< 0 car l'objet est généralement situé à gauche de la lentille et la lumière se dirige toujours de l'objet vers la lentille.
Distance image :
OA'> 0
Je ne vois pas comment faire l'équation pour démontrer
JE reposte la 3, j'ai apporté quelques modifications pour rendre plus clair
3-relation de conjugaison:
=0
4-Les racines de ce polynômes doivent être réelles pour avoir une signification physique . Le discriminant de ce polynôme doit donc être positif :
Δ=2−4.𝐷𝑓′=𝐷(𝐷−4𝑓′)>0 ⇔ D>4f'
5-A =
A=
Il y a donc 2 positions et
de la lentille, symétrique par rapport au plan médiateur de [𝐴𝐴′] qui permettent d'obtenir une image réelle de 𝐴.
On en déduit la distance =
séparant les deux positions de la lentille qui conduisent à deux images réelles
et à la distance
de l'objet 𝐴𝐵 :
soit