Inscription / Connexion Nouveau Sujet
Exercice sur le mouvement
Bonsoir,
J'ai besoin d'un coup de main pour cet exercice :
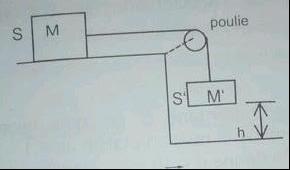
''Fil inextensible et sans masse. Poulie sans frottement et de masse négligeable. S' chute d'une hauteur h et S glisse d'une distance d avant de s'arrêter. Vitesse de départ nulle. Les frottements F (vecteur) sont supposés constants sur le plan horizontal.
(schéma joint en image)
1) Ecrire le théorème de l'énergie cinétique pour le système {S; fil et S'}.
2) Exprimer la valeur de la force de frottement F si M=1kg ; M'=5kg; h=0,1 m ; d=0,3 m.
4) calculer la vitesse maximale atteinte.
5) calculer l'accélération.
6) Calculer la tension du fil.
[bleu]
1) c'est cette question qui me bloque ... je ne sais pas comment déterminer l'énergie cinétique de l'ensemble du système :
J'ai commencé par diviser le système :
-solide (s)
En appliquant le théorème de l'énergie cinétique on a sachant que la vitesse finale est nulle:
-½*M*V²s=T*d-F*d où T est la tension du fil sur la masse M.
-solide (s')
On a : -½*M'*V²s'=T'd+M'*g*h
Mais alors comment l'écrire pour tout le système ...
Je complète ....
Quand on choisit {S + S' + fil + poulie} comme système étudié, la tension du fil est une force interne.
Je pense aussi que la vitesse initiale de S et le même que celle de S' , puis je donc élimininer les vitesses entre ces deux relation pour avoir une expression?
Finalement, mon absence est différée.
Question 1 :
Je pense qu'il faut distinguer 2 phases :
a) entre le départ et l'arrivée de S'
b) Après l'arrivée de S'
La vitesse "V" de S est la même en fin de phase 1 et au début de phase 2
Tu appliques le théorème de l'énergie cinétique au système {S + S'} pour la phase 1
et tu l'appliques à nouveau pour la phase 2.
En phase 2 le système se réduit à S puisque le fil est détendu.
Tu devrais obtenir 2 relations contenant les 2 inconnues "f" et "V" qui sont l'objet des questions 2 et 3
À la phase 1: soit Vo la vitesse initiale de de M' : Entre le départ et l'arrivée de s' on a pour le système s; s'
½M'V²-½M'Vo²=M'gh-F*d
À la phase 2
½M'V'²-½M'V²=M'gh ; avec V' la vitesse finale de s' qui sera nulle à l'arrêt .
À la phase 1: soit Vo la vitesse initiale de de M' : Entre le départ et l'arrivée de s' on a pour le système s; s'
½M'V²-½M'Vo²=M'gh-F*d
À la phase 2
½M'V'²-½M'V²=M'gh ; avec V' la vitesse finale de s' qui sera nulle à l'arrêt .
½M'V'²-½M'V²=M'gh-F*d
A mon avis :
Phase 1
S et S' partent du repos.
Ils sont animés à chaque instant de la même vitesse, laquelle atteint sa valeur maximale V lorsque S' entre en contact avec le sol.
Au cours de cette phase S et S' ont parcouru, l'un horizontalement, l'autre verticalement la même distance " h "
Soient Eci et Ecf les énergies cinétiques initiales et finales de l'ensemble (S+S')
On a donc :
Eci = 0
Ecf = (1/2) (M + M') V²
2 forces travaillent pendant cette phase : le poids de S' et la force de frottement
qui s'exerce sur S:
= M' g h ;
= -f h
Le théorème de l'énergie cinétique appliqué à cette phase 1 s'écrit :
soit
(1/2) (M + M') V² - 0 = M' g h - f h = h (M' g - f)
--------------------------------------------------------------------------------
Phase 2 :
Le fil s'étant détendu le système étudié n'est plus composé que de S, lequel part avec la vitesse V, se déplace d'une distance "d" et finit avec une vitesse nulle.
On ne se préoccupera pas ici de S' qui est maintenant immobile.
Je te laisse poursuivre.
À la phase 2:
l'énergie cinétique initiale de S est Eci=½MV² . le solide s s'arrête après un parcours de d mètres aucours duquel la seule force ayant travaillé est f . Donc Ecf=0
on a donc 0- ½MV²=-fd
je pense que c'est assez pour la question 1
2) Expression de f
Pour cela j'elimine V entre les deux relations precedentes
je trouve f=M'gh(h+d+M'd/M)^(-1)
A ce niveau j'ai tiré v² de la deuxieme relation de l'énergie cinétique de => v²=2fd/M ... je remplace cette relation dans la première : on a
1/2(M+M')(2fd/M)=M'gh-fh de là, f=M'gh(h+d+M'd/M)^(-1)
En application numerique je trouve f=9.31 N
4-calcul de la vitesse maximale
je pense que cette vitesse maximale est V ; on sait que 1/M2v²=2fd => v=²=2fd/M
En a application numérique v=2.36 m/S
5- calcul de l'accélération
En supposant ce qu'on demande est l'accélération du système s+s' , le mouvement étant uniformement varié on peut appliquer la relation v²-v'²=2ah où v' est la vitesse initiale qui est nulle , v la vitesse maximale et a l'accélération des deux solides. Ainsi v²=2ah => a=v²/2h ; A.N: a=27.84 m/s²
6- Tension du fil
Appliquons le théorème du centre d'inertie à la masse M: les forces extérieures sont : le poids, la tension du fil et la force de frottement f. on a donc suivant le sens du mouvement -f+T=Ma => T=Ma+f ce qui donne en application numérique T=37.15 N
Je suis d'accord avec tes résultats littéraux , mais pas avec tes résultats numériques.
Question 2 :
J'ai trouvé
Cette expression est équivalente à celle que tu proposes, mais en prenant g=9,8 m/s² j'obtiens f=2,58N
je vois l'erreur, en fait j'ai dû oublié l'exposant -1 de l'expression entre parenthèse. Je trouve aussi 2,58 à l'arrondi d'ordre 2.
Autrement dit les calculs sont à reprendre... L'essentiel étant acquis ... ça gêne pas trop 
Merci beaucoup à vous !
Il y a tout de même une différence entre ton résultat et le mien.
Tu trouves 2,58 là où je trouve 2,58N




