Inscription / Connexion Nouveau Sujet
Exercice sur la diffraction
Bonjour, j'ai un exercice à faire que je ne comprends pas...
L'objectif de cet exercice est de mesurer l'épaisseur inconnue d'un fil en s'appuyant sur des données expérimentales.
Pour cela, on utiliser un laser, produisant une lumière de longueur d'onde ƛ, placé devant une fente de largeur a.
On observe sur un écran, placé à la distance D de la fente, une figure de diffraction, constituée de taches lumineuses.
La largeur de la tache centrale L sur l'écran varie lorsque l'on fait varier :
-la longueur d'onde ƛ de la source monochromatique;
-la largeur a de la fente;
-la distance D entre la fente et l'écran.
Plusieurs séries d'expériences sont menées, les résultats sont les suivants :
-si la longueur d'onde augmente, alors la largeur de la tache centrale augmente;
-si la distance D augmente, alors la largeur de la tache centrale augmente.
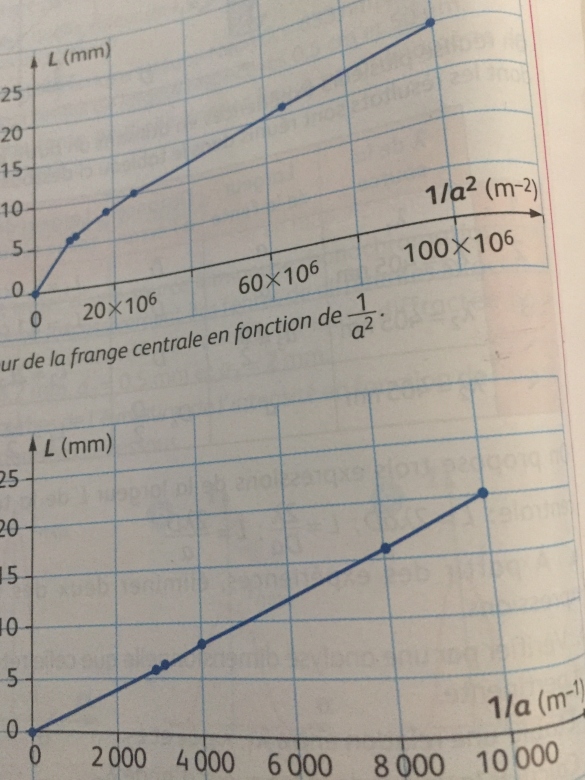
Lorsque l'on fait varier la largeur a de la fente. On obtient les courbes a et b.
1.a Quel phénomène est mis en évidence ?
b. A l'aide de l'ensemble des résultats expérimentaux donnés en énoncé, retrouver la bonne expression de L (k est une constante sans dimension):
L = kaDƛ
L = (aD)/ƛ
L = k(ƛD)/a
L=k(ƛD2)/a2
L= k(ƛa)/D
c. En déduire l'une des courbes la valeur de k, sachant que c'est un entier et que l'on a fait les mesures pour ƛ = 633nm et D=1,60m.
2.On remplace la fente précédente par un fil d'épaisseur inconnue a' (la figure de diffraction d'un fil est identique à celle d'une fente). On se place dans les conditions suivantes: ƛ=633nm et D=1,60m. La valeur de la tache centrale mesurée sur l'écran est L = 20mm.
Déterminer l'épaisseur a' du fil.
1.a Le phénomène mis en évidence est la diffraction : on observe une tache centrale avec des extinctions de lumière.
2.C'est à partir de là que je bloque...
Merci de m'aider !
Bonjour
Remplacer une fente de largeur "a" par un fil de diamètre "a" conduit à la même figure de diffraction. Pour la question 2, il suffit de reprendre l'étude précédente en remplaçant a par a'.
Tu avais écris dans ton premier message que tu bloquais à la question 2...
Un peu d'aide tout de même pour 1b :
L'énoncé précise que L est une fonction croissante de 
et de D. et D figurent nécessairement au numérateur de l'expression de L. Cela permet déjà d'éliminer certaines propositions.
Restent alors à savoir si le dénominateur fait intervenir a ou a2. On trace alors la courbe L = f(1/a) et la courbe L=g(1/a2). L'une est une droite, pas l'autre : que peux-tu en conclure ?
Tu peux alors déterminer le coefficient directeur de la droite et en déduire k.
Je te laisse réfléchir et proposer une solution.
Annuler
connectez vous