Inscription / Connexion Nouveau Sujet
Exercice optique lentilles
Bonjour,
Je cale sur un problème d'optique.
Voici la question:
Un objet doit doubler sa taille à travers une lentille convergente d'une distance focale de 8cm.
a) déterminez graphiquement où il faut placer l'objet? Déduisez-en la position de l'image.
b) vérifiez votre construction par calcul
c) Calculez la distance entre l'objet et l'endroit où l'image se forme
d) Sans changer la distance entre l'objet et l'image, où faudrait-il placer la lentille pour obtenir à nouveau une image nette? Dans ce cas que vaut ce grossissement?
Voila ce que je trouve:
a)Comment est-ce possible de le faire graphiquement sans aucun calcul?...
b) Soit f la distance focale, p la distance objet-centre optique et f' la distance centre optique-image, g le grandissement
J'ai que :
1/f = 1/p'-1/p
g = p'/p
Donc:
1/8 = 1/p'-1/p
2 = p'/p
Par subst. j'obtiens: p = -8 et p'= -16
je ne sais pas du tout si c'est correct, mais j'aurais jamais pu le trouver graphiquement je pense :/
c) J'ai du mal à interpreter ma solution, j'ai l'impression que mon image est derrière mon objet...
d) Alors là je sèche vraiment!
Grand merci à ceux qui sauront m'aider,
Un matheux qui galère en physique.
Bonjour,
Optique géométrique : comme son nom l'indique il faut faire appel aux théorèmes de géométrie. En l'occurrence le théorème de Thalès et les théorèmes sur les triangles semblables sont d'un usage permanent...
À cause de la question d) je suppose que l'image à obtenir doit être une image réelle.
Question a :
Parmi les trois rayons qui permettent de construire une image, je te conseille de réfléchir sur le rayon qui passe par le foyer objet. Cela te donne immédiatement la position de l'objet par rapport à la lentille (et donc la distance en notant O le centre optique de la lentille et A le pied de l'objet).
Je te signale que je n'utilise jamais l'expression que tu emploies. Elle est une source d'erreurs permanente.
Formule de conjugaison pour une lentille mince de centre O, formule dite de Descartes
Le pied de l'objet est en A
Le pied de l'image est en A'
Le foyer image est en F'
L'axe optique est orienté (dans le sens de propagation de la lumière)
avec ,
,
etc. les mesures algébriques des segments correspondants (l'axe optique étant orienté).

Il me semble que pour répondre à la question a la figure suivante est suffisante :
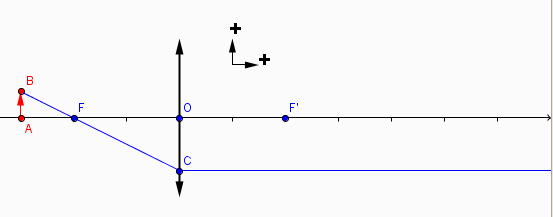
Sont importants sur cette figure les deux petits vecteurs (qui ne sont pas unitaires) qui indiquent le sens positif choisi selon l'axe optique et dans une direction perpendiculaire à cet axe.
OC = 2  AB
AB
Et... théorème de Thalès !
Mais il est bien préférable d'écrire :
Que vaut en conséquence AF ?
Sachant que l'énoncé te donne la distance focale de la lentille convergente :
Où doit se trouver l'objet, c'est-à-dire que vaut ? (attention au signe ! )

Bonjour, voici un problème posé par ma prof de physique:
Un objet doit doubler sa taille à travers une lentille convergente d'une distance focale de 8cm.
a) déterminez graphiquement où il faut placer l'objet? Déduisez-en la position de l'image.
b) vérifiez votre construction par calcul
c) Calculez la distance entre l'objet et l'endroit où l'image se forme
d) Sans changer la distance entre l'objet et l'image, où faudrait-il placer la lentille pour obtenir à nouveau une image nette? Dans ce cas que vaut ce grossissement?
a) Entre le foyer objet et le centre optique. Se sais que mon image sera virtuelle et agrandie de 2x et l'image sera droite.
b) p = -4 et p' = -8
c) elle est de -4, c'est a dire l'objet est virtuel et situé a 4cm derrière l'objet
d) AUCUNE IDEE! C'est pourquoi j'ai posté ma question. Je sais juste que pour que l'image soit la plus nette possible il faut travailler au voisinage de l'axe principal.
Si quelqu'un pourrait m'aider ce serait génial!
Merci.
*** message déplacé ***
Bonsoir,
Pour c, la distance est 4cm, sauf si tu parles d'une distance algébrique et dans ce cas c'est effectivement -4.
Je te donne un indice: la nouvelle image est réelle.
*** message déplacé ***


