Inscription / Connexion Nouveau Sujet
Exercice constante d’équilibre
Bonjour,
J'ai un exercice à faire sur la constante d'équilibre, mais j'ai du mal à réaliser les questions car j'ai encore un peu de mal avec certaines notions. Voici l'énoncé en espérant que vous pourrez m'aider:
Les ions iodure et plomb réagissent pour former de l'iodure de plomb. La transformation est modélisée par deux réactions opposées.
Pb2+(aq)+2I-(aq)->PbI2(s) (il s'agit de la flèche allant dans les deux sens).
A 25C, la constante d'équilibre est K(25C)=7,4*10^^7. On dissous totalement dans de l'eau distillée une masse m1=5,0g d'iodure de potassium et m2=5,0g de nitrate de plomb. Le volume de la solution est V =50,0mL.
1) Déterminer s'il se forme des cristaux d'iodure de plomb.
J'avoue que je ne vois pas pour cette question comment pouvoir y
répondre.. Je suppose qu'il faudrait utiliser les masse donné mais j'en suis pas sûr.
2) Lorsque le système n'évolue plus [Pb2+]f=1,5*10^^-3 lol/Let [I-]=3,0*10^^-3 mol/L. Calculer le taux d'avancement final et le quotient de réaction à l'état final À. Conclure.
J'ai commencé par calculer les quantités de matières des deux réactifs :
n (I-)=3,0*10^^-3*50*10^^-3
Or il y a deux mol de ions iodure donc n(I-)=7,5*10^^-5 mol
n(Pb2+)=1,5*10^^-3*50*10^^-3= 7,5*10^^-3 mol
Je sais que pour calculer le taux d'avancement il faut faire xf/xmax mais j'ai du mal à savoir que vaut xf et que vaut xmax...
Ensuite je calcul le quotient de réaction:
Qr,A=1/[Pb2+]*[I-]^^2=7,4*10^^7
Je ne sais pas vraiment comment conclure, mais on voit que Qr,A est égal à la constante d'équilibre a 25C.
Je voudrais déjà faire ces deux questions pour pouvoir essayer de trouver la suite..
Merci beaucoup d'avance !
Bonjour vanoise, effectivement il est dans mon programme. Je viens de comprendre que pour la question 1) il faudrait savoir le sens d'évolution du système pour savoir s'il y aura formation ou non des cristaux d'iodure de plomb.
Pour cela, il faudrait que je trouve Qr et que je vois si il est inférieur, supérieur ou égal à K, n'est ce pas ?
a réponse à ma question précédente est sûrement oui puisque tu utilises cette notion aux questions suivantes. Pour la première question : il suffit donc de comparer la constante d'équilibre au quotient initial calculé dans les conditions suivantes : les concentrations en ions sont égales aux concentrations initiales et on suppose l'existence d'un minuscule cristal de iodure de plomb. Si le sens spontané de la réaction correspond à la dissolution du solide, tu pourra conclure que le solide est instable dans ces conditions : la solution ne contient pas de solide, la solution n'est pas saturée.
Si le sens spontané correspond à la formation de solide : la solution est saturée : du précipité apparaît dans le bécher.
Mon message précédent a été écrit avant que je ne lise ton message de 14h13... Je pense que tu as compris.
Pardon, oui on aborde le quotient de réaction dans le programme.
Donc il faudrait que je calcul Qr,i mais comment savoir la concentration des ions à l'état initial?
De plus il faut bien que j'utilise la formule:
Qr=[C]^^c*[D]^^d/[A]^^a*[B]^^b ?
Donc il faudrait que je calcul les concentrations en ions iodure et plomb à l'état initial et d'après ce que vous m'avez dis, les concentrations en ions sont égales au concentrations initiales.
Mais comment calculer ces concentrations ?
Connaissant les masses de solides dissous ainsi que le volume de la solution, tu peux calculer les concentrations initiales en ions.
Pour l'expression de Qr : tu dois savoir que parler de concentration d'un solide n'a pas de sens. Lorsqu'un solide est présent, quelle qu'en soit la quantité, tu remplaces la concentration par "1" dans l'expression de Qr. Tu as déjà rencontré une situation analogue concernant l'eau dans une solution aqueuse diluée. Ici, en présence de solide, même en quantité infinitésimale :
Bon.. J'ai pris du temps à comprendre qu'il fallait que je me serve des masses données dans l'énoncé. Donc j'ai enfin calculé les concentrations :
[I-]=(m/M)/V=6,0*10^^-1
[Pb2+]=3,0*10^^-1
Donc j'ai pu calculer Qr,i=1/(6,0*10^^-1)^^2*3,0*10^^-1=9,3
Donc le sens d'évolution du système est direct: il y'a alors formation de cristaux d'iodure de plomb.
Oui ! Assez facile car, connaissant le volume constant de la solution, tu peux trouver facilement les quantités finales. Les quantités initiales sont connues.
J'ai fais le tableau d'avancement, et je trouve Xmax=7,5*10^^-3 mol
J'avais calculé plus haut que Xf=7,5*10^^-5 mol.
Donc on peut calculer le taux d'avancement:
T=Xf/Xmax=7,5*10^^-5/7,5*10^^-3=1,0*10^-2
Donc pour conclure la transformation est limitée.. je ne sais pas trop quoi conclure d'autre.
De plus Qr,À=7,4*10^^7
Pas d'accord avec tout ce que tu as écrit. Peux-tu indiquer les quantités initiales des réactifs ?
La constante d'équilibre étant très grande devant 1, il faut s'attendre à un taux d'avancement peu inférieur à 100%.
Attention aux unités mais c'est bien cela !
| espèces chimiques | Pb2+(aq) | I-(aq) | PbI2(s) |
| Quantités introduites (mol) | 1,5.10-2 | 3,0.10-2 | 0 |
| Quantités finales (mol) | 1,5.10-2-xf=7,5.10-5 | 3,0.10-2-2xf=15.10-5 | xf |
Cela devrait t'aider !
Je viens de me rendre compte que j'ai inverser mes valeurs dans mon tableau, mais je ne comprend toujours pas votre dernière ligne.
Donc j'ai:
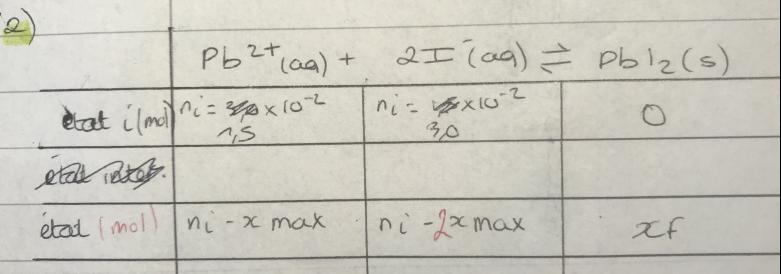
Je vous avoue que j'ai un peu du mal à comprendre la. Pouvez vous m'expliquer précisément ce que vous avez fait ?
Quantité finale d'ions plomb(II) :
nf(Pb2+)=[Pb2+]f.V=1.5.10-3*50.10-3=7,5.10-5mol
Raisonnement analogue pour les ions iodure. Cela justifie le tableau d'avancement. On obtient :
xf=1.49.10-2mol
Le mélange initial est stœchiométrique : il n'y a pas de réactif limitant : si la réaction était totale, les deux réactifs disparaîtraient en même temps.
xmax =ni(Pb2+)=1,5.10-2mol.
Je te laisse calculer le taux d'avancement.
D'accord, donc pour nf(I-)=1,5*10^^-4 mol.
On obtient xf=1,49*10^^-2 mol car:
Si Pb2+ (aq) est le réactif limitant:
ni(Pb2+)-nf(Pb2+)=1,49*10^^-2 mol
Si I-(aq) est le réactif limitant:
ni(I-)-nf(I-)=2,9*10^^-2 mol
Le réactif limitant est donc Pb2+(aq) avec xf=1,49*10^^-2 mol
Ensuite xmax=1,5*10^^-2 mol car Pb2+(aq) a la valeur de xmax la plus faible ?
Dans ce cas là T=xf/xmax=0,99. On considère qu'elle est totale car très proche de 1 où elle est quand même limitée ?
Si on raisonne sur l'ion plomb(II), on obtient :
1,5.10-2-xmax = 0
Si on raisonne sur l'ion iodure, on obtient :
3,0.10-2-2xmax=0
Ces deux calculs conduisent à la même valeur de xmax : logique dans la mesure où le mélange initial est réalisé dans les proportions stœchiométriques.
Ah oui effectivement. Donc pour conclure, cette transformation est totale puisque T=99%, et que Qr,À=K.
D'accord avec ton message de 18h37.
Pour les autres questions, si elles ont un rapport avec cet exercice, tu peux les poster dans ce sujet. Si elles portent sur autre chose, il faut créer un nouveau sujet.


