Inscription / Connexion Nouveau Sujet
étude mécanique
Bonjour,
Cela fait un petit bout de temps que j'essaie de faire cet exercice de physique mais j'aurais besoin de votre aide. 
Le voici :
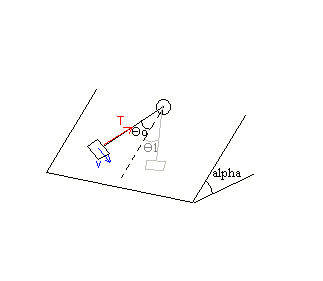
On considère un objet de masse m pouvantglisser sur unplan incliné d'un angle
par rapport à l'horizontale. Il est attaché à une ficelle extensible, elle-même fixée à l'autre extrémité à un point fixe, de sorte que la ficelle soit en permanence parallèle au plan incliné. La longueur entre le point d'attache fixe et le centre de gravité de l'objet est L. On négligera tout action de l'air.
L'objet subit de la part du support des frottements solides vérifiant la loi de frottement de Coulomb. En permanence, lorsque l'objet glisse, la norme F de la force de forttement vérifie F= 
N, où est un coefficient de frottement, sans unité, et N est la norme de la réaction normale du support. On négligera toute action de l'air.
L'objet est lâché sans vitesse initiale, le pendule faisant un angle 
0 avec la ligne de plus grande pente du plan incliné. Il remonte jusqu'à une hauteur inférieure, changeant de sens lorsque le pendule fait un angle 1 avec la ligne de plus grande pente du plan incliné. On va chercher à exprimer en fonction de ces angles là.
a)Déterminer l'expression de la norme de la réaction normale du support, notée N(qui ne dépend pas du mouvement de l'objet). En déduire l'expression de F lors du glissement.
b)La force de frottements vectF n'est pas une force constante, mais une force de norme constante et dont la direction par rapport à la trajectoire de l'objet reste constante. On admettra que son travail lors d'un déplacement s'écrit comme sa norme, multipliée pa la longueur du déplacement, multipliée par le cosinus de l'angle (constant) ente la tangente à la trajectoire et vectF.
A l'aide d'une étude mécanique appropriée, déterminer l'expression de en fonction de ,0,1.
c)On donne,0=60°,1=32° et =30°. Calculer .
d)Pour un autre type de matériau, on a =0,10. On règle =30° et0=60°. Déterminer 1, puis2, l'angle que fait le pendule avec la ligne de plus grande pente du plan incliné lorsqu'il remonte après son aller-retour. Montrer qu'il n'y a pas de 3, c'est à dire que l'étude qu'on a faite, supposant l'objet en glissement, n'est plus valable, c'est à dire encore que le pendule s'arrête.
Tout d'abord j'ai du mal à comprendre cette partie de l'énoncé : "le pendule faisant un angle 0 avec la ligne de plus grande pente du plan incliné. Il remonte jusqu'à une hauteur inférieure, changeant de sens lorsque le pendule fait un angle 1 avec la ligne de plus grande pente du plan incliné." Comment le complexe ficelle+objet peut il faire un angle avec la ligne de plus grande pente (que pense que c'est c'est verte sur mon dessin). Comment change t il de sens cet objet? Où sont les deux angles 0 et 1?
De plus, si l'objet remonte, alors le sens des frottements est changé puisqu'ils sont opposés au mouvement non? Pourtant à la question b) il est écrit "La force de frottements vectF n'est pas une force constante, mais une force de norme constante et dont la direction par rapport à la trajectoire de l'objet reste constante"
Tout cela pour pouvoir faire la suite, pour laquelle je pense, j'aurai encore des questions à vous poser..
Merci d'avance pour votre aide, je l'espère, suivie.
Le schéma en perspective nous donne (si je ne me suis pas trompé) :
ca permet d'expliquer simplement l'énoncé assez tordu il faut le dire...
Merci Je comprends mieux la situation !
a)
On étudie l'objet de masse m dans le référentiel terrestre supposé galiléen. Si on néglige l'action de l'air, sur l'objet s'exerce:
- son poids vectP vertical, vers le bas, de norme P=mg
-la réaction normale du support vectN, perpendiculaire au plan incliné, dirigée vers le haut, de norme N (avec N=F/)
-la force de frottement vectF, parallèle au plan incliné, de norme F (avec F=/N), dirigée vers où puisque ça change ? 
Quel théorème appliqué? Je dirais plutôt le théorème de l'énergie cinétique plutôt que la première loi de Newton étant donné que le système n' est pas immobile..
En considérant que mon introduction de l'étude mécanique soit juste, je continue :
On applique le théorème de l'énergie cinétique entre les point A, position initiale de l'objet avant d'être lâché sans vitesse initiale et B le point auquel l'objet se situe quand la ficelle fait un angle 1 avec la ligne de plus grande pente du plan avant de repartir en direction de A.
Ec(B)-Ec(A)= WAB(vectP)+ WAB(vectT)j'avais oublié la tension de la ficelle !+ WAB(vectF)+WAB(vectN)
Or j'aurais pensé que comme vectN est perpendiculaire au plan, cette force ne travaille pas mais on doit justement l'exprimer donc je me trompe, qu'en penses tu?
Donc je sais pas trop.
Es tu sûr qu'il faille utiliser ce théorème et non une loi de Newton? (1ère, 2ème ou 3ème)
Tu peux utiliser ce théorème ou bien la conservation de l'énergie mécanique aussi si tu veux. Ca reviendra au meme !
Bonsoir Romane,
Pour trouver N (normale au plan incliné), décompose P en deux composantes, une perpendiculaire au plan incliné (donc colinéaire à N) et l'autre parallèle au plan incliné.
Le travail de N est nul (perpendiculaire à la trajectoire).
Le travail de T est nul (perpendiculaire à la trajectoire).
Si tu calcules Ec(B) - Ec(A), à mon avis, ça ne va pas te mener loin parce que Ec(B) = Ec(A) = 0 puisque la vitesse est nulle aux points A et B (par hypothèse et si j'ai bien compris).
En revanche, il y a quelque chose qui me gêne dans le b).
N = P.cos(alpha)
F = Phi.N
F = Phi.P.cos(alpha)
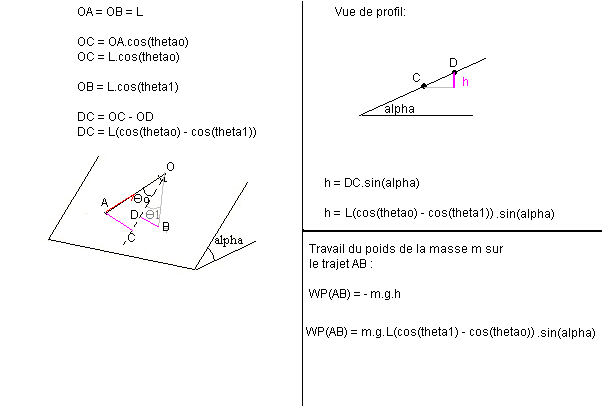
différence d'altitude entre les positions extrèmes de l'objet : Delta h
Delta h = L.[1-cos(theta0) - (1 - cos(theta1))].sin(alpha)
Delta h = L.(cos(theta1) - cos(theta0)).sin(alpha)
Travail du poids de l'objet sur ce trajet: WP = mg.Delta h
WP = mg.L.(cos(theta1) - cos(theta0)).sin(alpha)
Travail de frottement = - F.L.(theta0 - theta1) = -Phi.P.cos(alpha) . L.(theta0 - theta1)
Et donc:
mg.L.(cos(theta1) - cos(theta0)).sin(alpha) = Phi.mg.cos(alpha) . L.(theta0 - theta1)
(cos(theta1) - cos(theta0)).sin(alpha) = Phi.cos(alpha).(theta0 - theta1)
Phi = tan(alpha) * (cos(theta1) - cos(theta0))/(theta0 - theta1)
-----
Phi = tan(alpha) * (cos(theta1) - cos(theta0))/(theta0 - theta1)
Phi = tan(30°) * (cos(32°) - cos(60°))/(Pi/3 - (32/180).Pi)
Phi = 0,41
-----
Rien relu, comme d'habitude.
Marc 35! Merci à toi d'intervenir, ainsi qu'à J-P
Le travail de T est nul car perpendiculaire à la trajectoire? moi je dirais plutôt parallèle.. Qu'est ce qui te gène dans le b)? Quelle loi de Newton utiliser si ce n'est pas le théo de l'Ecinétique?
J-P je vais lire tout ça et essayer de comprendre Tu appliques le théorème de l'Ecinétique?
Le travail de T est nul car perpendiculaire à la trajectoire? moi je dirais plutôt parallèle..
Non, non, perpendiculaire.
ha oui, et en permanence en plus a)Déterminer l'expression de la norme de la réaction normale du support, notée N(qui ne dépend pas du mouvement de l'objet). En déduire l'expression de F lors du glissement.
J-P, j'ai bien lu ton message de 15:29 or je ne comprends pas à quoi correspond quoi, de plus pourrais tu faire un schéma rapide qui indique comment tu fais la trigonométrie? Il faut en faire un "de profil" et non en 3D je suppose..
"Déterminer l'expression de la norme de la réaction normale du support, notée N(qui ne dépend pas du mouvement de l'objet)" --> ton résultat trouvé est N = P.cos(alpha)?
"En déduire l'expression de F lors du glissement"--> tu trouves F = Phi.P.cos(alpha)?
Mais comment?
As tu traité les questions b) et c)? Où commence ta réponse à chacune d'elle?
Merci beaucoup
cf message de 21:53
Ensuite erreur de signe dans mon message précédent.
La force de frottement est f = Phi.N
Et N = P.cos(alpha) = mg.cos(alpha)
--> f = Phi.mg.cos(alpha)
f est à tout moment dans la direction de la vitesse de la masse mais de sens opposé.
f est donc sur tout le trajet tangentielle à la trajectoire de la masse.
Et donc l'angle fait entre f et la trajectoire est à tout moment de 180°
Le travail de la force de frottement est donc:
Wf = f.arc(AB).cos(180°)
Wf = - f.arc(AB)
Et arc(AB) = L(|theta0| + |theta1|) -->
Wf = - Phi.mg.L.cos(alpha).(|theta0| + |theta1|)
-------
Comme le mobile est arrété en A et en B, (énergie cinétique de m est = 0 en ces points)
On a : WP + Wf = 0
et donc:
mg.L.(cos(theta1) - cos(theta0)).sin(alpha) = Phi.mg.L.cos(alpha) .(|theta0| + |theta1|)
Phi = [(cos(theta1) - cos(theta0)).tan(alpha)]/(|theta0| + |theta1|)
Phi = [(cos(32°) - cos(60°)).tan(30°)]/(92/180)*Pi)
Phi = 0,125
Aux nouvelles distractions ou erreurs près.
Bonsoir J-P je te remercie beaucoup d'avoir pris de temps d'écrire tout ça
C'est assez clair pour moi, mais comme d'habitude il y a quelques petites choses que je ne saisis pas du premier coup:
1)Qu'est ce que le point D? Tu supposes que l'objet remonte plus haut qu'au point de sa position initiale je pense, mais pourquoi?
2)Tu écris W(AB)=-mgh, pourquoi un -? Et pourquoi disparait il dans la ligne suivante?
3)Comment sais tu que N = P.cos(alpha) = mg.cos(alpha)? C'est donc la réponse à "Déterminer l'expression de la norme de la réaction normale du support, notée N(qui ne dépend pas du mouvement de l'objet)"
4)f = Phi.mg.cos(alpha) est donc la réponse à "En déduire l'expression de F lors du glissement."
5)Je ne comprends pas comment tu trouves "Wf = f.arc(AB).cos(180°) soit Wf = - f.arc(AB)", qu'est ce que l'arc? Pourquoi le signe - apparait puis disparait? Pour moi le travail d'une force = norme*longueur du trajet parcouru*cos(angle)
C'est tout pour l'instant
Merci encore
Tu supposes que l'objet remonte plus haut qu'au point de sa position initiale je pense, mais pourquoi?
Mal lu l'énoncé : "Il remonte jusqu'à une hauteur inférieure"
Restent les questions 2),3),4),5) mais prend ton temps
Le point D est la projection orthogonale du point B sur OC.
C'est un artifice utilisé pour calculer la diddérence d'altitude entre les points A et B.
Et c'est à cause du dessin imprécis que D est plus haut que C.
Ce devrait être le contraire ...
Il n'est pas exclus qu'il y ait des erreurs de signe dans ma réponse (que je n'ai de nouveau pas relue) à cause de cela...
Vérifie donc bien le tout.
En voila déjà modifiées sur le dessin.
Mais il en reste sûrement d'autres.
2)Je ne pense pas que cela soit une erreur de signe..
3)4)Je ne comprends pas ta démarche trigonométrique. Comment as tu trouvé cela?
5)Je n'ai jamais utilisé la notion d'arc
Toutes les erreurs de signe n'ont pas été corrigées.
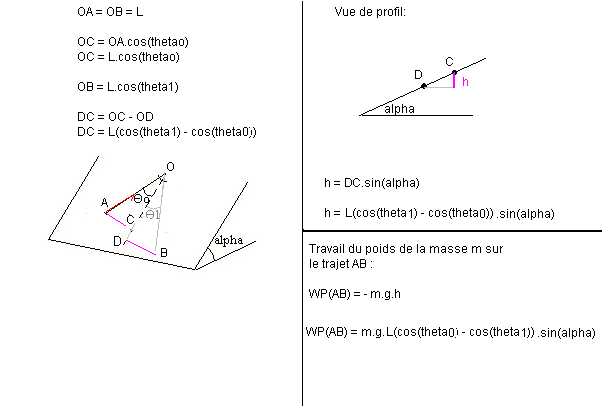
h = L.(cos(theta1) - cos(theta0)).sin(alpha)
h étant la différence d'altitude entre les points A et B.
WP = mgh = mgL.(cos(theta1) - cos(theta0)).sin(alpha)
-----
Le poids de l'objet peut être décomposé en 2 composantes.
L'une normale au plan incliné (en bleu sur le dessin).
L'autre suivant la ligne de plus grande pente du plan incliné.
La composante bleue du poids est compensée par la composante N (en vert sur le dessin) de la réaction du support.
Et donc N = P.cos(alpha) = mg.cos(alpha)
---
L'énoncé dit que = la norme F de la force de frottement vérifie F = Phi. N ...
Et donc |F| = Phi.mg.cos(alpha)
---
Merci beaucoup ! J'ai tout bien compris.. sauf que :
je ne comprends pas comment tu trouves "Wf = f.arc(AB).cos(180°) soit Wf = - f.arc(AB)", qu'est ce que l'arc? Pourquoi le signe - apparait puis disparait? Pour moi le travail d'une force = norme*longueur du trajet parcouru*cos(angle)
J'ai compris ce que c'était que l'arc AB.. voir dessin
Quelle formule te permet d'affirmer que l'arc(AB) = L(|theta0| + |theta1|) ?
Bonjour J-P, peut être as tu oublié cet exercice ou peut être trouves tu que je suis trop longue à comprendre.. dans tous les cas j'aimerais savoir pourquoi tu mets un signe négatif dans la deuxième ligne de ce calcul :
Wf = f.arc(AB).cos(180°)
Wf = - f.arc(AB)
et d'après quelle formule tu écris ceci : Et arc(AB) = L(|theta0| + |theta1|) (mathématiques)
Merci bien
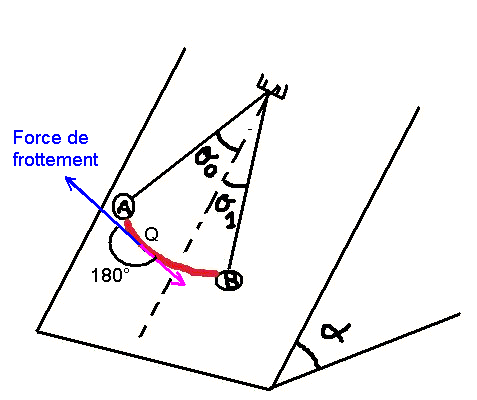
En n'importe quel point Q de la trajectoire du mobile, la force de frottement est de même direction et de sens contraire à la vitesse instantanée et donc aussi au déplacement élémentaire du mobile en ce point.
Et donc sur le trajet AB:
Wf = - f.arc(AB)
D'accord
Est ce que la valeur Phi = 0,125 est toujours valable après les modifications que tu avais apportés (signes) ?
A la dernière question d) c'est dans cette expression dont je ne suis pas sure de la justesse à cause des erreurs (petites ) qu'on avait faites : Phi = [(cos(theta1) - cos(theta0)).tan(alpha)]/(|theta0| + |theta1|) qu'il faut remplacer les données alpha, phi et theta 0?
Je ne comprends pas ce qu'est que l'angle theta 3..
d)
Phi=0,10. On règle alpha=30° et theta0=60°. Déterminer theta1, puis theta2,
Phi = [(cos(theta1) - cos(theta0)).tan(alpha)]/(|theta0| + |theta1|)
0,1 = [(cos(theta1) - cos(60°)).tan(30°)]/(|Pi/3| + |theta1|)
--> par méthode graphique, on trouve theta1 = 0,652 rad (soit 43,74°)
-----
Le pendule repart alors dans l'autre sens avec un angle initial de theta 1 et jusque un angle theta 2 tel que :
Phi = [(cos(theta2) - cos(theta1)).tan(alpha)]/(|theta1| + |theta2|)
0,1 = [(cos(theta2) - cos(43,74°)).tan(30°)]/(|0,652| + |theta2|)
--> par méthode graphique, on trouve theta2 = 0,2905 rad (soit 16,6°)
-----
Il reste à vérifier que la force de frottement est maintenant suffisante que pour empêcher le pendule de repartir dans l'autre sens ...
Et donc qu'il n'existe pas d'angle theta 3.
Cela peut aussi se faire en vérifiant que l'équation :
Phi = [(cos(x) - cos(theta2)).tan(alpha)]/(|x| + |theta2|) n'a pas de solution.
0,1 = [(cos(x) - cos(16,6°)).tan(30°)]/(|0,2905| + |x|)
On trace la courbe de f(x) = [(cos(x) - cos(16,6°)).tan(30°)]/(|0,2905| + |x|) - 0,1 sur une calculette graphique par exemple ...
Et on constate que cette courbe ne coupe pas l'axe des abscisses.
Donc il n'y a pas de valeur de x pour laquelle : f(x) = 0, soit pas de valeur de x pour laquelle on aurait:
0,1 = [(cos(x) - cos(16,6°)).tan(30°)]/(|0,2905| + |x|)
--> pas d'angle theta 3 possible.
-----
Sauf distraction ou erreur.
Avant de passer à ton dernier message je voudrais revenir sur ton message de 20:13, plus precisément les calculs avec les dessins.
Je pense que DC= OD-OC et non OC-OD et tu as marqué DC=L(cos(theta0)-cos(theta1)) Du coup.. ça change l'expression de h et donc de WP(AB) et donc toute ta question d) de 10:24...
Qu'en penses tu?
Je n'en pense rien, pas le courage de tout relire.
Corrige ce qui doit être corrigé dans les signes ...
Mais Le travail du poids sur AB est positif. (puisque A est à une altitude supérieure à celle de B).
Et voir message du 17-01-10 à 11:2
WP = mgL.(cos(theta1) - cos(theta0)).sin(alpha) est bien positif... Cela semble donc bon.
Le travail de frottement (sur le trajet (AB) est négatif est donc
Wf = - Phi.mg.cos(alpha) * L(|theta0| + |theta1|)
me semble bon aussi.
Et comme le mobile est à vitesse nulle en A et en B, on a :
WP + Wf = 0
soit:
mgL.(cos(theta1) - cos(theta0)).sin(alpha) - Phi.mg.cos(alpha) * L(|theta0| + |theta1|) = 0
(cos(theta1) - cos(theta0)).sin(alpha) = Phi.cos(alpha)*(|theta0| + |theta1|)
qui aboutit bien à :
Phi = [(cos(theta1) - cos(theta0)).tan(alpha)]/(|theta0| + |theta1|)
formule déjà utilisée depuis le message du 16-01-10 à 18:57
-----
Annuler
connectez vous