Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

étude mécanique

Posté par
-Romane- 30-11-09 à 22:35

Bonsoir,
pourriez vous m'aider à faire cette étude mécanique ? J'ai commencé mais "ça s'essoufle vite"..

Voici l'énoncé :

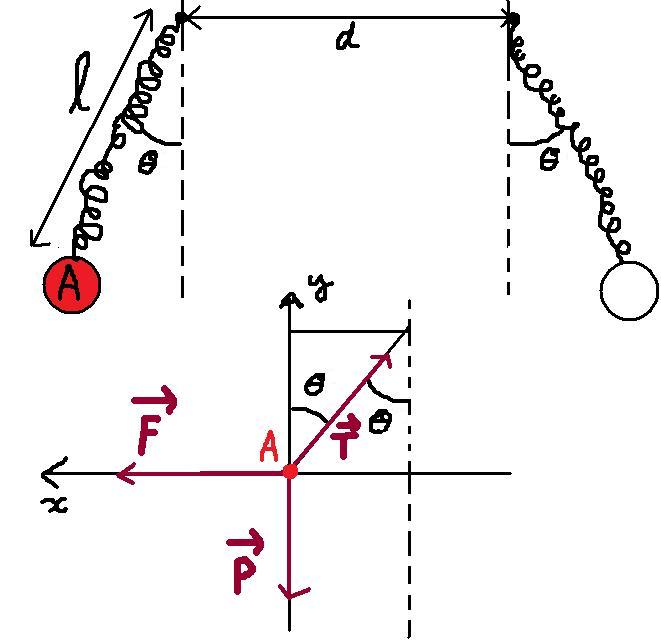
Deux ressorts identiques de longueur au repos l0 et de raideur K sont attachés à des points fixes situés à la même hauteur et distants de d. A l'autre extrémité de chacun des ressorts sont fixés deux boules de masse m et portant une charge q identique. A l'équilibre, les ressorts prennent chacun une longueur l et font un angle par rapport à la verticale.
Déterminer une équation impliquant , m, g, K, l0, d, q et k (constante intervenant de la force électrostatique).
Déterminer numériquement (à l'aide de la calculatrice) lorsque K=10N/m, q=1,0.10^-5 C, l0= 0,10m, d=1,0m, m=0,10kg, g=10 N/kg et k=9,0.10^9 U.S.I.

Tout d'abord, je me demande si on peut considérer que la distance entre les deux boules est d (?).


On étudie la boule A dans le référentiel terrestre supposé galiléen munit d'un repère (0;;) où est "colinéaire à d et dirigé vers la gauche, horzontal, et "perpendiculaire  à d" et vertical vers le haut. La boule est ramenée à son centre d'inertie.
Comment reformuler ce qui est entre guillemets ?

Sur elle s'exercent :
-son poids vectP, perpendiculaire vers le bas de norme P = mg
-la tension du ressort vectT de norme T = K(l-l0)
-la force qu'elle subit de la part de l'autre boule vectF dirigé vers la gauche (car force répulsive)et horizontal et de norme F = kq²/d²

Coordonnées des vecteurs :
vectP(0, -mg)
vectF(kq²/d²; 0)
vectT(K(l-l0)sin;K(l-l0)cos)

Le boule est le ressorts étant à l'équilibre on peut appliquer la première loi sur Newton:
vect P + vect T + vectF = vecteur nul
sur (O;) on a Kq²/d² = K(l-l0)sin
sur (O;) on a -mg = K(l-l0)cos
C'est juste tout ça?

Ensuite je n'arrive pas à faire un mixte de ces deux égalités afin de déterminer une équation impliquant , m, g, K, l0, d, q et k...

Merci beaucoup

étude mécanique

Posté par
Marc35re : étude mécanique 30-11-09 à 22:57

Bonsoir,
"Tout d'abord, je me demande si on peut considérer que la distance entre les deux boules est d (?)." ==> Non
"sur (O;) on a Kq²/d² = K(l-l0)sin" ==>  Kq²/d² est faux (d n'est pas la distance entre les boules)

Posté par
122155re : étude mécanique 30-11-09 à 23:09

Salut:
-  l'expression de la force éléctrostatique:
F =k.\frac{q^2}{D^2}  avec D=d+2.l.sin           à corriger

équilibre

\vec{P}+\vec{T}+\vec{F}=\vec{0}
sur (O;) :     Kq²/D² = K(l-l0)sin       correct
sur (O;) :      -mg + K(l-l0)cos=0      à corriger

étude mécanique

Posté par
-Romane-re : étude mécanique 02-12-09 à 17:23

Merci beaucoup pour ta réponse qui me fait bien avancer.
Je me retrouve donc avec les deux égalités
kq²/(d+2lsin)²=K(l-l0)sin
et
K(l-l0)cos=mg
Sauf que je j'ai beau remplacer tout par tout je n'arrive pas à déterminer une équation impliquant , m, g, K, l0, d, q et k. Tu peux me donner un coup de pouce?

Posté par
122155re : étude mécanique 03-12-09 à 18:05

\frac{kq^2}{(d+2lsin\theta)^2}=K(l-l_0)sin\theta  (1)

K(l-l0)cos=mg  (2)    


(2)  ===> K(l-l_0)=\frac{m.g}{cos\theta}
et tu remplace dans (1) qui devient:


\frac{kq^2}{(d+2lsin\theta)^2}=m.g. tg\theta

Posté par
-Romane-re : étude mécanique 03-12-09 à 20:07

Il y a un petit hic : l0 n'apparait pas dans l'équation alors qu'il devrait et l doit disparaitre
Moi aussi j'avais fait comme toi mais ça ne va pas...
Que faire?

Posté par
Marc35re : étude mécanique 04-12-09 à 13:18

Il suffit de faire  l\,=\,l_0\,+\,\frac{m\,g}{K\,cos\theta}
\frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2}=m.g.%20tg\theta
Et on a bien "une équation impliquant , m, g, K, l0, d, q et k"

Maintenant, pour en tirer , le calcul me semble ardu mais...

Posté par
-Romane-re : étude mécanique 04-12-09 à 20:39

Pour l'instant je comprends
Par contre j'ai essayé "d'extraire de cette équation" mais à chaque fois que trouve une expression différente ... peux tu me guider?
Ca serait très aimable

Posté par
Marc35re : étude mécanique 04-12-09 à 20:49

Pour le moment, je n'ai pas réussi...

Posté par
-Romane-re : étude mécanique 04-12-09 à 20:57

Si tu trouves fais moi signe

Posté par
Marc35re : étude mécanique 04-12-09 à 21:03

OK

Posté par
-Romane-re : étude mécanique 04-12-09 à 21:09

Je crois bien que le prof a dit qu'on serait obligé de se servir de la calculatrice pour résoudre cette équation (cad trouver la valeur de theta) mais j'ai jamais fait ce genre de chose !

Posté par
Marc35re : étude mécanique 04-12-09 à 21:34

Je l'ai tournée dans tous les sens et il me reste toujours un sin et une tan.
Donc la résolution n'a pas l'air simple ou il y a une ruse "infâme" pour réussir à la mettre sous la bonne forme.

Posté par
-Romane-re : étude mécanique 04-12-09 à 21:37

Et une calculatrice ne peut pas le faire?

Citation :
à l'aide de la calculatrice
Laisse sous entendre qu'il faut le faire avec non?
Peut être que 12215 sait

Posté par
Marc35re : étude mécanique 04-12-09 à 21:58

Il faut peut-être utiliser la calculatrice ?...
On peut peut-être tracer les courbes représentatives des deux membres de l'équation pour trouver une solution graphique approchée et affiner ensuite par le calcul...

Posté par
-Romane-re : étude mécanique 04-12-09 à 22:13

Je ne  comprends pas ta méthode, tu peux la reformuler s'il te plait? enfin expliquer

Posté par
Marc35re : étude mécanique 04-12-09 à 22:49

Je pense qu'on peut tracer \frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2}  et tracer  m.g.%20tan\theta  en fonction de , bien entendu.
Sur le graphique, on peut voir si les courbes se croisent d'abord et ensuite trouver sur le graphique une valeur approchée.
A partir de cette valeur approchée, on peut trouver une valeur plus fine par calcul en faisant des petits incréments en bouclant le calcul plusieurs fois.
Le calcul à faire est \frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2}  et m.g.%20tan\theta en les comparant jusqu'à obtenir une égalité acceptable en faisant varier par petits incréments dans un sens ou dans l'autre. Mais il faut avoir une idée de la solution pour ne pas partir d'une valeur trop éloignée de la solution.
Avec une calculatrice, je ne sais pas si c'est faisable (il faut programmer les formules sinon on en a pour un moment ! ). Il y a longtemps que j'ai oublié comment on programme une calculatrice. J'utiliserais plutôt un tableur ou un programme en C.

Posté par
Marc35re : étude mécanique 04-12-09 à 22:56

J'essaierai de trouver la solution par programme mais pas ce soir, il est trop tard

Posté par
-Romane-re : étude mécanique 04-12-09 à 23:00

Je vais essayer de comprendre ton explication. Je reviendrai demain. A demain?
merci encore, et si tu n'as pas le temps ça ne fait rien..

Posté par
Marc35re : étude mécanique 05-12-09 à 14:56

Je vais essayer de faire un programme mais je vais tenter à nouveau le calcul... mais je n'y crois pas trop...

Posté par
-Romane-re : étude mécanique 05-12-09 à 15:03

Je ne sais pas utiliser un solveur avec une calculatrice, et toi?

Posté par
Marc35re : étude mécanique 05-12-09 à 15:32

J'ai calculé :
\frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2}\,-\,m\,g\,tan\theta
qui devrait être égal à 0 idéalement.

Avec un résultat de 2.10-8, je trouve = 0.485786 rad  soit 27,8° environ

sauf erreur éventuelle de ma part...

Posté par
Marc35re : étude mécanique 05-12-09 à 15:37

Un solveur ?... J'ai dû essayer sur la mienne pour des équations du 4ème ou 5ème degré.
Mais, sauf erreur de ma part, c'est pour résoudre les équations de polynômes, même une équation de degré 25.
Mais là, ce n'est pas tout à fait ce que l'on a...

Posté par
Marc35re : étude mécanique 05-12-09 à 15:46

J'ai écrit un programme en langage C pour faire le calcul mais tu peux très bien faire un programme sur la calculatrice qui calcule cette formule... comme tu connais à peu près la réponse...
Si tu te rappelles comment on fait un programme sur une calculatrice (en ce qui me concerne, j'ai oublié mais ce n'est pas très difficile).
Tu rentres dans le programme une valeur de que tu modifies avec le pas approprié et tu relances plusieurs fois le programme jusqu'à obtenir un "zéro" acceptable (=> 2.10-8 en ce qui me concerne).

Posté par
-Romane-re : étude mécanique 05-12-09 à 16:00

Je ne sais pas ce que c'est qu'un programme ni comment l'utiliser.
(J'ai une TI-82 stats.fr)
Tu as trouvé une valeur de theta?

Posté par
J-Pre : étude mécanique 05-12-09 à 16:25

0,541428 rad, soit 31,02°

Posté par
-Romane-re : étude mécanique 05-12-09 à 16:34

J-P, tu peux m'expliquer comment tu as fait?
Merci encore à vous deux

Posté par
Marc35re : étude mécanique 05-12-09 à 17:32

Bon, je me suis peut-être trompé... Je vérifierai mon programme

Posté par
-Romane-re : étude mécanique 05-12-09 à 17:34

Posté par
J-Pre : étude mécanique 05-12-09 à 18:25

Tracer la courbe du message du 05-12-09 à 15:32

f(theta) = k.q²/ ... sur une calculette graphique et voir à quelle valeur de theta elle vaut 0.

Ou bien avec un tableur (Excel)

Voila un zoom de la courbe dans la zone intéressante :

étude mécanique

Posté par
-Romane-re : étude mécanique 05-12-09 à 18:43

Pourquoi passe t on le mg tan theta de l'autre côté?
qu'est ce que f(theta)? Pourquoi le fait de savoir pour quelle valeur de theta (dans l'expression de 15:32) l'expression vaut 0 nous donne la valeur de theta?
merci

Posté par
J-Pre : étude mécanique 05-12-09 à 18:54

Le message du 04-12-09 à 22:49 dit :

Le calcul à faire est \frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2} et m.g.tan\theta en les comparant jusqu'à obtenir une égalité.

Il revient au même de chercher pour quelle valeur de theta, on a:
\frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2} = m.g.tan\theta que de chercher la valeur de theta pour laquelle :

\frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2} - m.g.tan\theta = 0

On trace donc la courbe de f(\theta) = \frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2} - m.g.tan\theta et on regarde sur le graphe la valeur de alpha pour laquelle f(\theta) s'annulle.

Posté par
J-Pre : étude mécanique 05-12-09 à 18:59

Lire : valeur de theta pour laquelle ...


Posté par
-Romane-re : étude mécanique 05-12-09 à 19:08

Je comprends tout sauf le rapport entre la solution de l'équation (où l'inconnu est theta) et la veleur de theta pour laquelle f(theta) s'annule...

Posté par
Marc35re : étude mécanique 05-12-09 à 20:56

Oui, effectivement... 0,541428 rad...désolé, une erreur de parenthèse
Romane
La solution de l'équation
\frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2}%20=%20m.g.tan\theta
est la même que celle de l'équation
f(\theta)%20=%20\frac{kq^2}{(d+2(l_0\,+\,\frac{m\,g}{K\,cos\theta})sin\theta)^2}\,-\,m.g.tan\theta\,=\,0
Je ne sais pas si c'est ça, ton problème...

Posté par
-Romane-re : étude mécanique 05-12-09 à 21:04

C'est bon j'ai compris

Je passe à un exo de chimie, si ça vous dit et si vous avez le temps.. https://www.ilephysique.net/sujet-exercice-dosage-235292.html J'aimerais vraiment arriver à le faire

merci à vous

Posté par
Marc35re : étude mécanique 06-12-09 à 10:51

Pour la chimie, je ne suis pas un hyper-spécialiste.
Mais la réponse à la question 1 me semble particulièrement confuse.
NH2SO3H(s) + H2O(l) NH2SO3-(aq) + H3O+
La masse molaire de NH2SO3H étant 97 g, la quantité de matière est 1/97 mol.
Il en est de même pour NH2SO3- et H3O+ (d'après la réaction).
Pour calculer les concentrations, on a 200,0 mL soit  0,2.10-3 m3
[NH2SO3-] = [H3O+] = (1/97) / 0,2.10-3 mol.m-3
0 = i [Xi]
0 = H3O+ [H3O+] + NH]2SO3- [NH2SO3-]
0 = ((1/97) / 0,2.10-3) (35,0.10-3 + 4,83.10-3)  S.m-1

Qu'en penses-tu ?

Posté par
-Romane-re : étude mécanique 06-12-09 à 11:03

C'est très gentil de répondre à mon appel, il serait mieux de continuer sur le topic de l'exo de chimie pour ne pas tout mélanger
Par contre, Kaela m'a dit que la question 1) était juste.
Et puis, je ne comprends pas pourquoi la quantité de matière de NH2SO3- est la même que celle de H30+, on a calculé cette quantité de matière avec la masse molaire de NH2SO3H or H3O+ n'a pas la même masse molaire....
Pourquoi ne s'occupe t on pas de H2O?

Posté par
Marc35re : étude mécanique 06-12-09 à 12:04

Si tu te rappelles l'équilibre des équations et les tableaux d'avancement
                NH2SO3H(s) + H2O(l) NH2SO3-(aq) + H3O+
état initial   x mol         en excès         0 mol          0 mol
état final     0 mol         en excès         x mol          x mol

Dans le cas où la réaction est totale, bien sûr...

Posté par
-Romane-re : étude mécanique 06-12-09 à 12:19

Je pense que la question 1) est juste à présent : https://www.ilephysique.net/sujet-exercice-dosage-235292.html
Pourquoi dis tu que l'eau est en excès? Je croyais que c'était un solvant.

Posté par
Marc35re : étude mécanique 06-12-09 à 14:06

Citation :
Pourquoi dis tu que l'eau est en excès? Je croyais que c'était un solvant.

On pourrait mettre x mol de H2O et on aurait une équation équilibrée. On aurait juste la quantité d'eau nécessaire à la réaction. Si on en a moins, il reste du NH2SO3H solide.
L'eau est un solvant et un solvant est toujours en excès. C'est pour cela qu'on ne s'occupe pas de la quantité de H2O.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !