Inscription / Connexion Nouveau Sujet
Etude énergétique
Bonjour, j'ai un doute sur une formule, et mes résultats ne sont pas corrects.
Voici l'énoncé complet :
I. Le pendule simple : étude énergétique à partir d'une vidéo.
A partir de la vidéo PenduleSimple.avi :
- Ouvrir cette vidéo avec Aviméca ou regavi.
- Etalonner soigneusement l'image et prendre comme origine, la position d'équilibre de la
masselotte ( sa position la plus basse)
- Pointer les positions de la masselotte sur deux périodes au moins.
- Transférer vers Régressi. (Si vous n'avez pas regavi placé dans le même dossier que
Regressi, ouvrez d'abord regressi puis transférez )
Masse de la masselotte : m = 38g
a. Déterminer la période du mouvement.
b. Créer deux nouvelles grandeurs : vx la vitesse selon l'axe des abscisses et vy la vitesse
selon l'axe des ordonnées. Comment les calcule-t-on ?
c. Rappeler l'expression de la norme du vecteur vitesse v à partir de vx et vy.
d.Tracer l'évolution de l'énergie cinétique de la masselotte en fonction du temps.
Que vaut sa période de Ec? Comparer à celle du mouvement.
e. Donner la valeur maximale de l'énergie cinétique Ec. A quelle position du pendule
correspond-elle ? Comment varie l'énergie cinétique au cours d'une oscillation ?
f. Tracer l'évolution de l'énergie potentielle de pesanteur de la masselotte en fonction du
temps. Que vaut sa période ? Comparer à celle déterminée en a.
g. Donner la valeur maximale de l'énergie potentielle de pesanteur Epp. A quelle position du
pendule correspond-elle ? Comment varie l'énergie potentielle de pesanteur au cours d'une
oscillation ?
d. Tracer l'évolution de l'énergie mécanique Em de la masselotte en fonction du temps.
Conclure.
A la question c. j'ai un doute sur la formule, je pense que c'est mais je ne trouve pas le bon résultat par la suite lors du calcule de l'énerge cinétique, qui a pour formule Ec = 1/2m*v².
L'énergie cinétique s'annule deux fois par période et est maximale deux fois par période. Pour Ec, tu devrais trouver une sinusoïde de période égale à la moitié de la période du mouvement.
J'ignore quelle méthode tu utilises pour obtenir vx et vy : sans doute une méthode qui assimile le mouvement à un mouvement de vitesse constante entre deux points de mesure. Cette méthode introduit des erreurs mais pas à ce point là !
Te serais-t-il possible de poster le tableau où figurent les valeurs de t, de x et de y, de vx et de vy. Il serait alors sans doute possible de comprendre d'où vient le problème.
La longueur du pendule est-elle connue ?
Voici le tableau, il y a 130 lignes, directement tirées de Aviméca (pour les deux premières colonnes). La longueur du pendule ne varie pas.
Pas très lisible tout cela ! Tu ne pourrais pas par hasard exporter tes données dans un tableur type Excel ou LibreOffice ? Sinon, tu pourrais peut-être faire une copie d'écran avec zoom...
J'ai fais quelques vérifications : tu as choisi semble-t-il m=38kg et non trente-huit grammes mais cela n'explique pas pourquoi, les valeurs de vx, vy , Ec deviennent beaucoup trop faibles au bout d'une demie période alors qu'elles semble cohérentes sur la première demie période. x et y varient périodiquement ; il devrait en être de même de toutes les autres grandeurs.
Difficile d'en dire plus en l'état.
Bonjour, j'ai exporté les valeur vers un Google Sheet disponible ici
comme ça, vous verrez mieux
PS, je vais corriger la masse à 0.038 kg
Merci ! Tout est parfaitement lisible maintenant. Je vais regarder cela de plus près cet après-midi.
Bonjour,
Je m'incruste...
Pourrais-tu poster le mémo de l'onglet expressions pour voir s'il n'y a pas de faute de frappe.
(un simple copier-coller suffit)
Bonjour gts2
'Pointages AviMéca
vx=x/t
vy=y/t
Ec=0.019*(vx^2+vy^2)
voici
Merci vanoise pour votre aide.
Je viens d'étudier tes valeurs. Seules les valeurs des vitesses au voisinage de t= 0 sont correctes puis les erreurs deviennent de plus en plus importantes. Je te rappelle comment calculer , du moins de façon approchée, une vitesse . en notant 
t=0,04s la durée entre deux mesures :
la vitesse à la date tn s'écrit :
Les logiciels de mécanique font ce genre de calculs.
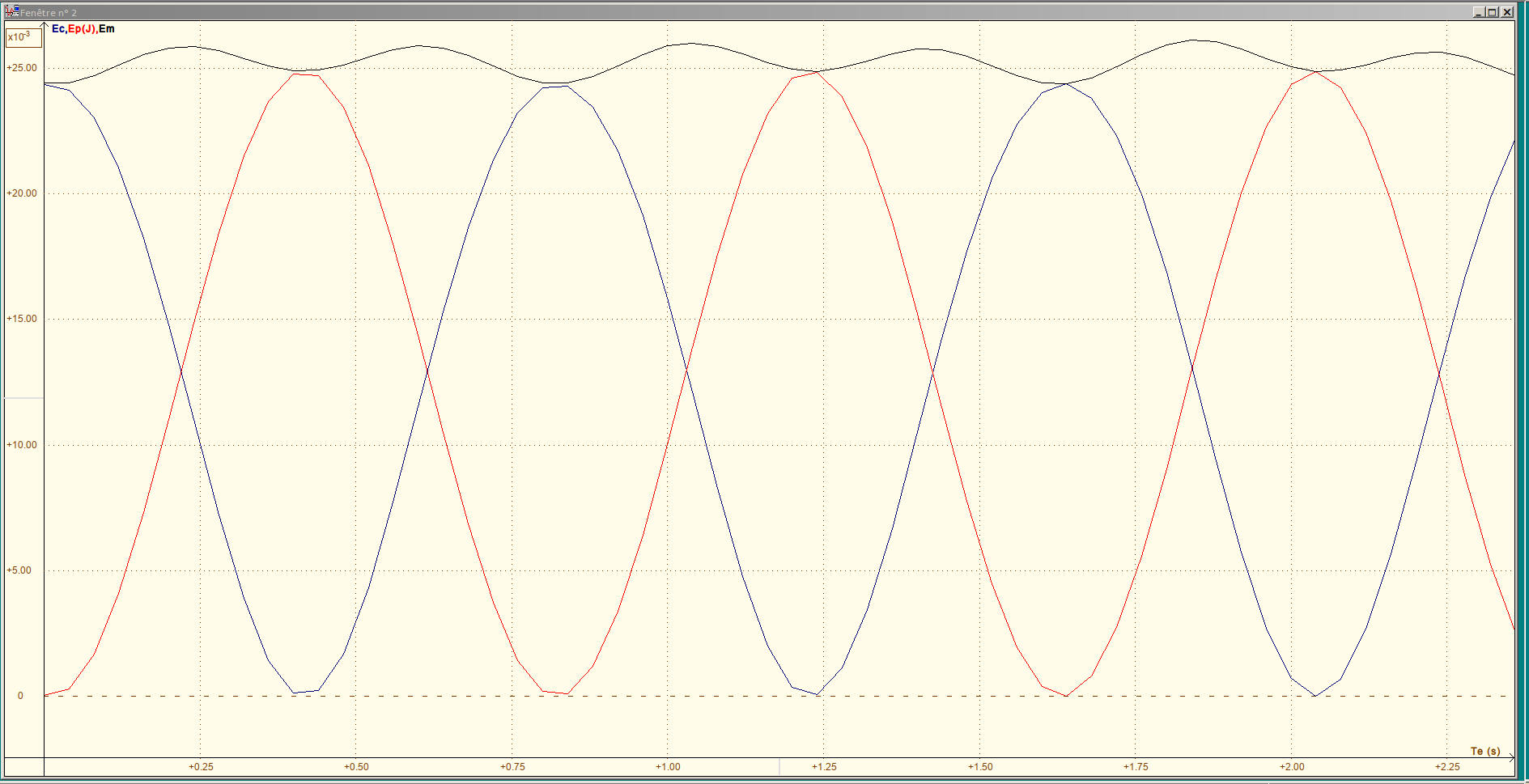
Tes valeurs de x et de y en fonction de t sont satisfaisantes. Par curiosité, j'ai représenté dans le même repère les variations en fonction du temps de Ec, de Ep=m.g.y et de Em=Ec+Ep. (Image pas top : juste une copie d'écran)
On voit bien qu'à un maximum de Ec correspond un minimum de Ep et vice et versa.
L' énergie mécanique devrait être constante.En fait, on n'obtient pas une droite horizontale, on constate l'existence d'ondulations de faible amplitude : approximations dans les calculs de vitesse et les acquisitions introduisent aussi de faibles erreurs.
Merci beaucoup, en fait pour calculer la vitesse il suffit de faire d étant la dérivé, et la d'un coup ça marche beaucoup mieux.
Si je connaissais mes cours ce serait plus simple.
Bref la vitesse sur l'axe des x c'est la dérivé de la x par rapport au temps, de même pour y.
Je mets quand même la capture de ce que j'obtiens pour être sur que c'est bon.
Par contre je n'obtient pas de courbe à peu près droite pour Em, c'est a cause de Epp qui est trop faible, pourtant c'est bien Epp = mgz soit Epp= 0.038*9.8*y
Au temps pour moi, je logiciel a mal choisi les unitées donc c'est pour ça. Et j'ai remplacé un + par un * aussi. Mais bon ça marche, la courbe Em est très capricieuse mais elle est là, presque constante.
Tu as bien pensé à utiliser m=0,038kg dans l'expression de Ec ?
Tu peux indiquer la valeur de Ec(max) et la valeur de Ep(max) ? J'obtiens dans les deux cas, des valeurs proches de 0,025J.
Annuler
connectez vous