Inscription / Connexion Nouveau Sujet
Etude de la charge d'un condensateur à travers une résistance
Bonjour,
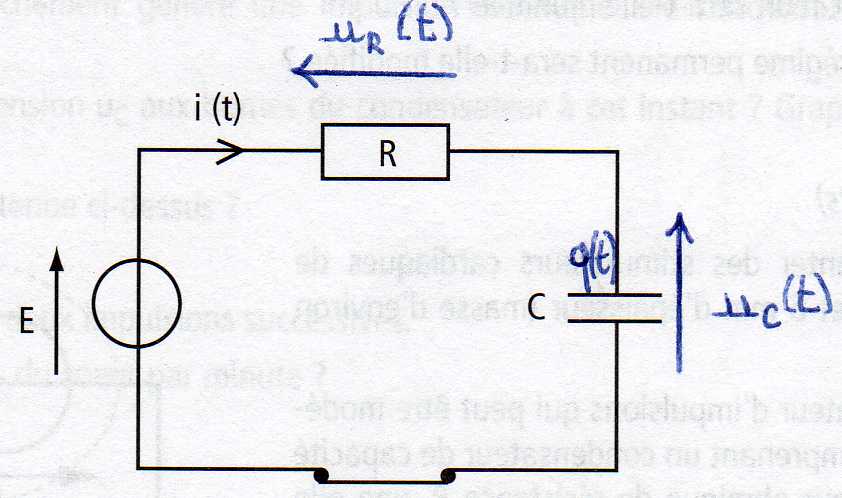
J'étudie la charge et la décharge d'un condensateur à travers une résistance R dont le schéma est joint plus bas. Je ne comprends pas très bien comment on trouve les formules.
Commencons par l'étude théorique de la charge :
A l'instant t = 0s on ferme l'interrupteur. On suppose qu'initialement le condensateur est déchargé
la charge du condensateur q(0) = 0 autrement dit la tension uc(0) = 0
On utilise alors la loi des mailles qui s'écrit :
E - uR(t) - uc(t) = 0
----> utilise-t-on cette relation uniquement lorsque le condensateur est initialement déchargé (car lorsque le condensateur est initialement chargé on utilise aussi la loi des mailles mais elle ne s'écrit pas du tout pareil) ?
Par la loi d'ohm aux bornes de R, uR(t) = Ri(t)
Ensuite on dit que uR(t)= RC car il existe une relation entre i, C et
selon laquelle i =
= C
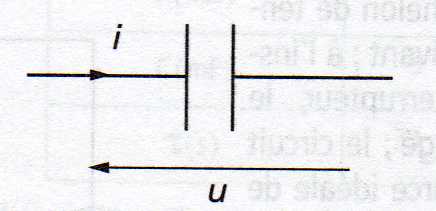
lorsque l'intensité I et la tension une direction de sens contraire (voir le second schéma plus-bas)
D'où l'équation différentielle :
E = uC(t)+ RC
C'est là que je ne comprends pas :
commment en vient-on à obtenir la solution de cette équation différentielle uC(t)= + B ? Qu'est-ce A et B, les armatures ? d'où sort le
? et puis que représente ce "e" ?
Pourriez-vous m'expliquer s'il vous plaît ?
ou alors après avoir obtenu uC(t) comme on sait que la charge de l'armature est reliée à la tension selon la formule q(t) = CuC(t), on fait juste un petit calcul en plus.
pas la peine de répondre à ma dernière question (du message de 17h46)....
Bien essayons de prendre dans l'ordre :
- sur la loi des mailles :
E - uR(t) - uc(t) = 0 est vrai à tout moment t>0 . Je ne comprends pas c'que tu veux dire par "car lorsque le condensateur est initialement chargé on utilise aussi la loi des mailles mais elle ne s'écrit pas du tout pareil"
- pour la résolution de l'équation diff ... Je vois qu'il y a beaucoup de choses à voir. Si tu ne sais pas ce qu'est "e" , tu ferais mieux d'attendre. En début de terminale, tu ne peux rien comprendre dans tout ça c'est normal. Si tu veux vraiment prendre beaucoup d'avance je peux t'en dire un peu plus mais tu as beaucoup de chapitre de maths à faire avant d'arriver à comprendre. Sache néanmoins que A et B sont des constantes qui dépendent des conditions initiales entre autres.
- étudier la charge d'un condensateur, ce n'est pas étudier spécialement q. C'est étudier le comportement du condo pendant qu'il se charge. Etudier uc(t), q(t) ou i(t) c'est équivalent puisqu'ils sont reliés par des équations : q(t) = C.uC(t) ... pourquoi ? parce que c'est comme ça ^^ c'est la loi de comportement du condensateur au même titre que pour une résistance c'est u=R.i
Pourquoi utilisez les constantes A et B ? Ne pourriez-vous tout de même m'expliquer pour "e", c'est le nombre exponentielle n'est-ce pas ? mais je ne vois pas trop le rapport. De plus si on me donne la solution différentielle avec je ne vois pas comment faire le calcul dans le sens inverse, je veux dire retrouver l'équation différentielle à partir de la solution (différentielle).
Dans mon cours ils utilisent dans l'étude théorique de la charge (d'un condensateur à travers une résistance R) la loi des mailles écrit de la manière suivante : E - uR(t)-uC(t)= 0 et dans l'étude théorique de la décharge ils l'écrivent :
Les constantes A et B sont mathématiquement nécessaires. On appelle ça des constantes d'intégration. Si tu veux, une équa diff ne te donne pas une unique solution, on connait la forme des solutions mais il y a toujours une ou des constantes qui sont déterminées uniquement par les conditions initiales (condo chargé ou déchargé par exemple).
Le nombre e est le nombre exponentiel oui, il permet ici d'introduire la fonction exponentielle. Tu auras tout un chapitre dessus, tu peux regarder des fiches sur ce site pour en apprendre + mais je ne pense pas que ça soit nécessaire tout de suite.
On peut "deviner" l'expresssion de l'équation différentielle à partir de la solution quand elle est écrite comme ça, mais là encore tu ne peux pas le deviner. Ce que l'on pourrait faire si tu connaissais les propriétés de la fonction exponentielle, c'est vérifier que la solution proposée vérifie bien l'équa diff.
Enfin, tu me donnes deux équations à des niveaux différents dans tes dernieres lignes. La loi des mailles est toujours la loi des mailles, qu'on l'écrive dans la charge ou la décharge. Seulement pendant la décharge, on a E=0, c'est pourquoi cela qu'on a uR(t)+uC(t)= 0 d'où uc + RC duc/dt =0
Après avoir obtenu l'équation différentielle :
(là, j'ai compris le déroulement des différents calculs)
On admet la solution de l'équation différentielle :
(là je n'ai pas très bien compris comment on l'a obtenu, je ne saurai pas la retrouver, ni retrouver l'équation différentielle à partir de cette solution)
Et puis pourquoi ne pas écrire que :
?
De plus (toujours dans mon cours) il est écrit :
le terme RC a bien la dimension d'un temps ; nous retrouvons  = RC (Ok, j'ai compris)
= RC (Ok, j'ai compris)
Lorsque t tend vers l'infini, la tension uC(t) est constante et égale à E : B = E ; la solution s'écrit donc (là je ne comprends pas, pourquoi la constante B serait-elle égale à E ? A quoi donc nous servent les constantes A et B si après on les remplace par E et pour la constante A par -E ?)
Comment cela, dans l'étude de la charge (où le condensateur est initialement déchargé) on a E = uR(t) + uC(t) et pourquoi dans l'étude de la décharge (où le condensateur est initialement chargé) on aurait E = 0 si le condensateur est initialement chargé.
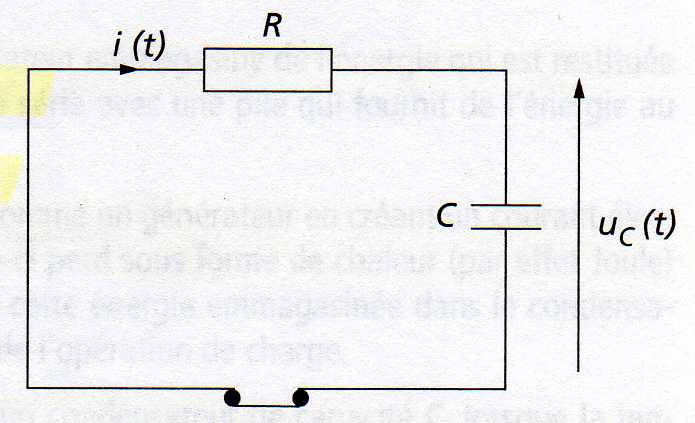
De plus dans le cas de l'étude théorique de la décharge sur le schéma ci-dessous n'apparaît pas le générateur, pourquoi ?
Bon on va essayer de le faire ... C'est un gros boulot ^^ accroche-toi
RC.du/dt + u = E
Pour résoudre cette équation (c'est à dire trouver u en fonction de constantes et de t), il faut d'abord résoudre RC.du/dt + u = 0.
Les solutions de cette équation sont de la forme u(t) = A.e-t/RC . C'est comme ça XD ça se justifie mathématiquement, mais au lycée tu auras à le retenir par coeur.
Ensuite il faut ajouter une constante qui tient compte du 2e membre (le "E" ). On remarque que : "Lorsque t tend vers l'infini, la tension uC(t) est constante et égale à E"
Donc E est en fait une solution particulière de notre équation. Du coup, la solution de notre équation RC.du/dt + u = 0 est u(t) = E + A.e-t/RC
On s'arrête et on souffle. On peut vérifier que cette solution est valable. Je te le dis mais tu ne le sais pas, que si on dérive e-t/RC, on trouve -1/RC . e-t/RC .
Donc si on remplace dans l'équa diff, on trouve :
RC (-A/RC . e-t/RC ) + E+ A.e-t/RC = E
Donc c'est valide.
Enfin, pour trouver A, il faut regarder la condition initiale : à t=0, on a u=0 donc 0 = E + A donc A = -E
Je pense que c'est assez dur à suivre et c'est normal, encore une fois tu n'as pas encore les bases pour suivre ce calcul
Tout simplement, si on laissait un générateur, le condensateur ne pourrait pas se décharger ... La décharge c'est justement quand le condensateur est libre de se décharger, sans qu'un générateur ne cherche à le recharger
Bon alors en imaginant qu'on charge un condensateur de capacité C à l'aide d'un générateur de f.e.m E et de résistance négligeable par l'intermédiaire d'une résistance R selon le premier schéma donné et qu'on cherche l'équation différentielle déterminant la charge q(t) du condensateur.
(exercice d'un devoir que je dois résoudre et envoyer à la correction)
Je suppose qu'on utilise là encore la constante A déterminée par les conditions initiales. D'après l'énoncé le condensateur est initialement déchargé, c'est bien ca ou je commence déjà à m'embrouiller ?
(pourriez-vous me guider, sans me donner la réponse, je voudrais essayer de le résoudre bien que je ne suis pas sûre d'avoir tout compris)
L'équation différentielle est obtenue à partir de l'étude du circuit : loi des mailles, loi des noeuds, loi de comportement d'un condo, loi d'ohm, ...
Tu vois qu'on te propose la même forme de solution, c'est normal les deux équations diff sont proches, seul le 2e membre et la condition initial diffèrent
donc, on suppose qu'initialement le condensateur est déchargé :
q(0) = 0 c'est-à-dire : uC(0) = 0
La loi des mailles s'écrit :
E - uR(t) - uC(t) = 0 avec uR(t) = Ri(t) =
avec  = RC donc uR(t) = Ri(t) =
= RC donc uR(t) = Ri(t) = 
= E
c'est bon jusque là ?
Quelle est la différence entre les constantes A et K ? est-ce parce que A c'est une constante d'intégration et K un coefficient de proportionnalité ?
Dans ce cas, le comportement du condensateur correspond-t-il bien à cette remarque :
Lorsqu'on ferme l'interrupteur, on remarque que la tension uC(t) croît rapidement puis devient constante : elle tend vers la tension du générateur E.
K est une constante d'intégration, A est la solution particulière, dans d'autres cas d'équation diff, A pourrait être fonction de t mais là c'est autre chose encore.
je ne comprends pas pourquoi tu écris uR(t) = R.i(t) = RC duC[/sub]/dt + u[sub]C = E
Le 2e égal est faux
a priori non ... ce n'est que quand tu connais uC(t) que tu peux en déduire ça, il manque un signe - d'ailleurs
J'ai écrit que uR(t) = Ri(t) (par la loi d'ohm) et Ri(t) = parce que la tension u du condensateur est dans le sens inverse de l'intensité i donc la relation entre i, C et du/dt s'établit de la manière suivante :
i = \frac{dq}{dt} = \frac{d(Cu)}{dt} = C\frac{du}{dt} et comme uR(t) = Ri(t)
ah oui, je vois. j'ai sauté une ligne...
Bon alors je récapitule :
J'ai :
q(0) = 0 comme q(t) = uc(t), uc(0) = 0
E - uR(t) - uc(t) = 0 avec uR(t) = Ri(t) =
Remplacons les différents membres :
E - - uc(t)= 0
d'où E = + uc(t)
Est-ce que l'équation différentielle permettant de déterminer la charge q(t) du condensateur s'écrit alors comme cela :
q(t) =
et si on me demandait de trouver la solution de cette équation différentielle (telle qu'elle est donnée dans l'énoncé) comment dois-je faire ?
ah, ok. Si ca ne vous dérange pas j'enverrai la suite de l'exercice (ce que j'ai su faire, que je n'ai pas compris ou su résoudre) demain. Je vais voir si j'arrive à comprendre mieux l'explication que vous m'avez donné à 20:59 aussi.
d'accord
si tu veux comprendre mieux et avoir des explications plus longues que les miennes, va sur :
https://www.ilemaths.net/maths_t_equations_differentielles_cours.php
Voilà juste avant de m'en aller (et de revenir demain après-midi, soir) je poste la suite de l'exo que j'ai fait :
La solution de cette équation différentielle s'écrit q(t) = A + Ke-t/RC
a) Lorsque t tend vers l'infini, la charge q(t) est constante. Exprimer cette charge en fonction de E et C.
J'ai écrit :
Lorsque t tend vers l'infini, la charge q(t) est constante et égale à E : A = E, la solution s'écrit donc : uC(t) = E + car le terme RC a une dimension d'un temps, nous retrouvons
 = RC.
= RC.
La constante K est déterminée par les conditions initiales à t = 0, uc(0) = 0 d'où uc0 = E + K = 0  K = -E
K = -E
On en déduit uC(t) = E (1 - )
Comme q(t) = CuC(t)
L'expression de cette charge en fonction de E et C est donc :
Est-ce juste ?
b) Exprimer la charge q(t) solution de l'équation différentielle sachant qu'à t = 0, on ferme l'interrupteur, le condensateur étant déchargé.
Là je ne vois pas quoi répondre, il me semble que j'y ai déjà répondu à la question précédente. Alors qu'elle différence y a-t-il entre ces deux questions ?
c) En déduire l'expression de l'intensité du courant dans le circuit.
J'ai répondu : i(t) =
Est-ce que c'est bon ?
Je vous remercie d'avance pour votre aide !
a) Ce que tu as fait est juste. Attention néanmoins, il y a des phrases bizarres :
"Lorsque t tend vers l'infini, la charge q(t) est constante et égale à E : A = E" tu mélanges uC(t) et q(t). q n'est pas homogène à E.
Néanmoins, je ne suis pas sûr que tu répondes à la question si ?
Si j'ai tout compris, on te dit :
"La solution de cette équation différentielle s'écrit q(t) = A + Ke-t/RCa) Lorsque t tend vers l'infini, la charge q(t) est constante. Exprimer cette charge en fonction de E et C."
b) voilà, là il faut faire ce que tu as fait à la question précédente. Dans a), on te demande juste ce qu'il se passe à t infini
c) tu as oublié un - ça fait : -e-t/
si la réponse à la question b) est alors que faut-il que je réponde à la question précédente où je dois exprimer la charge constante q(t)en fonction de E et C lorsque t tend vers l'infini? Je ne vois d'ailleurs pas très bien la différence entre les deux questions mis à part que dans a) t tend vers l'infini et dans b) t= 0 le condensateur étant déchargé.
D'autre part, pourquoi ne pourrais-je dire dans a) que la charge q(t) constante est égale à E, A = E ? A
si j'ai dit ca, c'est que dans mon cours ils écrivent la solution de l'équation différentielle :
uc(t) = (quand on suppose initialement le condensateur est déchargé et qu'à l'instant t = 0 on ferme l'interrupteur) et uc(t) =
lorsque t tend vers l'inifini (la tension uC(t) est constante et égale à E : B = E) et dans le devoir comme la formule de la solution de l'équation différentielle a la même forme sauf que c'est q(t)et les constantes d'intégration sont différente, j'en ai déduit que je pouvais faire de la même manière.
Puis-je écrire alors, que la tension uC(t) constante, lorsque t tend vers l'infini est égale à E : A = E ?
c) pourquoi y aurait-il un - devant ?
Dans la question a), on te demande sans calcul ou presque, de dire ce qu'il se passe quand t tend vers l'infini, c'est à dire quand le régime stationnaire est établi.
D'autre part, pourquoi ne pourrais-je dire dans a) que la charge q(t) constante est égale à E, A = E ?
Simplement par q c'est une charge et que E c'est une tension. Donc q ne peut pas être égal à E
La dérivée de e-t/
 est -1/
est -1/ . e-t/
. e-t/ c'est de là que vient le -
c'est de là que vient le -Donc pour la question a) je devrais plutôt répondre :
Lorsque t tend vers l'infini, la charge q(t) est constante. J'en déduis alors que la tension uC(t) est aussi constante (ou non ?) donc la tension uC(t) est égale à E : (est-ce que je peux dire là que A = E? ) la solution uCt = et étant donné que q(t) = uc(t)C la solution de l'équation différentielle à ce moment-là s'écrirait :
.
Est-ce exact ?
Et du coup pour la question b), je répondrai que la charge q(t) solution de l'équation différentielle où à t= 0, on ferme l'interrupteur, le condensateur étant déchargé, est de :
On te dit quoi ?
La solution de cette équation différentielle s'écrit q(t) = A + Ke-t/RC
a) Lorsque t tend vers l'infini, la charge q(t) est constante. Exprimer cette charge en fonction de E et C.
Quand t tend vers l'infini, Uc(t) tend vers E donc q(t) tend vers C.E. Par identification avec la solution proposée, on en déduit que A=C.E
C'est tout ce qu'il faut dire pour la a)
Il faut distinguer 2 choses :
Physiquement : Uc(t) tend vers E DONC q(t) tend vers C.E (car q(t) = C.Uc(t) )
Mathématiquement : la fonction q(t) = A + Ke-t/RC tend vers A en l'infini.
Donc A=C.E
Ah oui, ok j'ai compris pour le premier.
Est-ce toujours la constante A qui est définit par les conditions initiales (je veux dire dans la charge et décharge) ?
donc la constante A tend vers l'infini, la tension uc(t) est constante et égale à E.
La solution s'écrit uc(t) = Pourquoi A = C.E ?
et non A = -E puisque t = 0, uC(t) = 0 d'où uC(0) = E + A
... euh.. ca ne va pas me donner A = C
 E. Comment y êtes-vous parvenu ?
E. Comment y êtes-vous parvenu ?


