Bonjour, je bloque sur cet exercice.

ÉNONCÉ
Une piste ABC est formée de deux parties AB et BC situées dans un plan vertical.
AB est une portion circulaire de rayon r et de centre O, telle que :




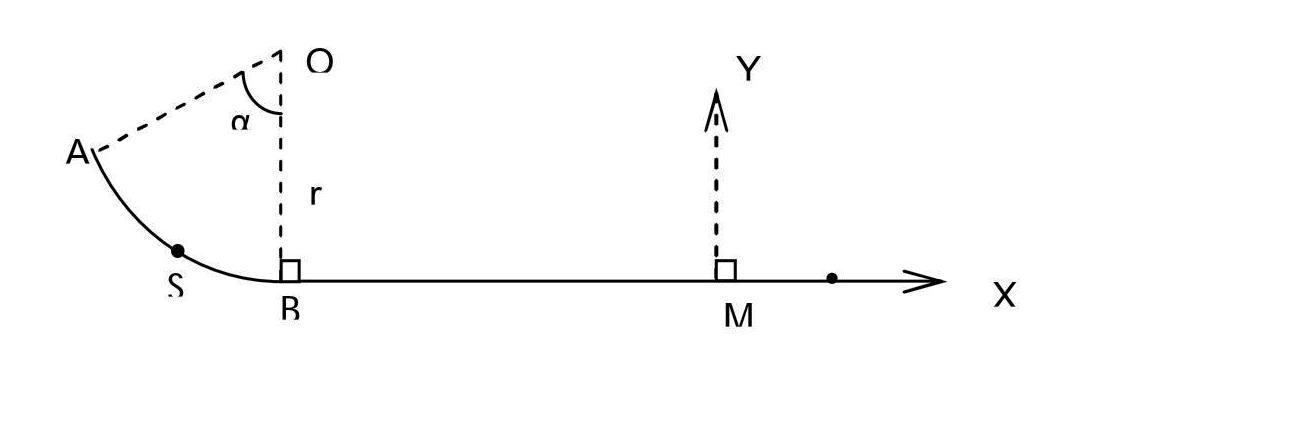
BC est une partie rectiligne horizontale.
Une bille de masse m = 150 g assimilée à un point matériel part sans vitesse initiale du point A et glisse le long de la piste ABC.
Il n'existe pas de frottement sur la portion AB.

1.Faire l'inventaire des forces extérieures agissant sur la bille entre A et B

2.1 En utilisant le théorème de l'énergie cinétique, déterminer l'expression de la vitesse de la bille en B en fonction de r, et g .

2.2 Calculer la valeur de la vitesse pour r = 0,75m ; = 30° ;  g = 10m.s-2

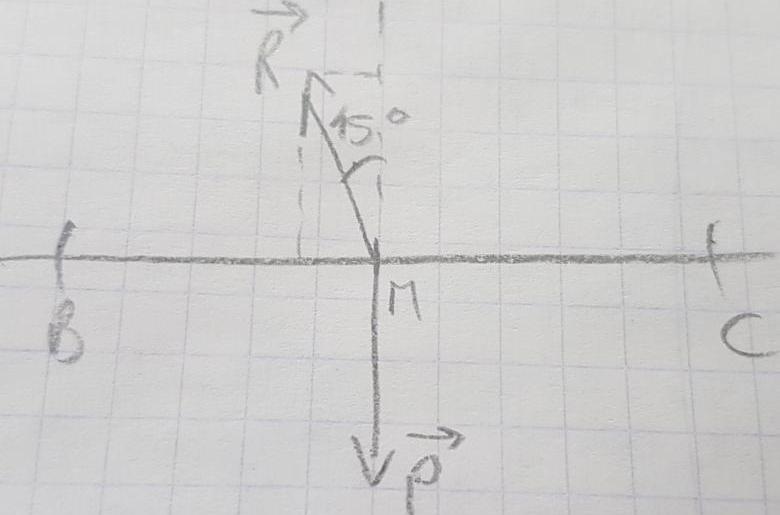
3. La bille évolue maintenant sur la partie BC. L'existence des forces de frottements fait que la réaction ܴ exercée par la piste sur la bille est inclinée d'un angle =15° Par rapport à la verticale .On suppose que la valeur de = 1,4ms-1

3.1 En appliquant le théorème du centre d'inertie à la bille :

3.1.1 Montrer que ܴ = .Calculer sa valeur

3.1.2. Établir l'expression de l'accélération en fonction de et g. Faire l'application numérique.

3.2 Déduire de la question 3.1.2 la nature du mouvement de la bille entre B et C

3.4 Établir l'équation horaire du mouvement, en considérant pour origine des espaces le point B et pour origine des dates, l'instant ou la bille passe en B.


Mes reponses

1.
Inventaire des forces extérieures : Le poids de la bille et la réaction normale de la piste

2.1. Je trouve =

2.2. = 1,41m/s

3.1. Je bloque à partir d'ici