Bonjour,

Je me permets de poster ici car j'ai une difficulté avec un aspect d'un exercice dont voici l'énoncé :

Une sphère conductrice de rayon 50 cm porte une charge de -4 C. On la place au centre d'une sphère creuse conductrice de 2,5 m de rayon externe, dont la cavité a un rayon de 1,5 m. La charge totale de la sphère creuse est de +12 C.

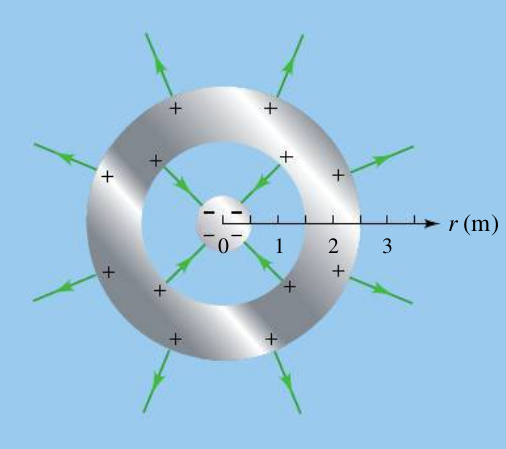
a) Représenter schématiquement la distribution des charges ainsi que les lignes de champ.

b) Calculer le module du champ électrique aux distances r suivantes du centre commun aux deux sphères : 3m, 2m, 1m, 10cm, 0.

J'ai un problème avec la partie b), plus précisément avec le calcul du module du champ à distance r = 1m du centre.

Mon problème est que je me dis que les charges positives réparties sur la surface interne de la sphère creuse (cf. figure) devraient produire un champ électrique de même module que le champ produit par les charges négatives réparties sur la surface externe de la petite sphère pleine, et que le champ électrique dans la cavité devrait être le champ résultant de l'addition de ces deux champs.

Autrement dit le champ électrique E en r = 1 m devrait être égal à E_int. + E_ext.

Or, d'après le corrigé de l'exercice, E = E_int (i.e. E est égal au champ produit par la petite sphère de charge - 4 C). Je me creuse la tête et je n'arrive pas à comprendre pourquoi...

J'espère avoir été clair... Merci d'avance pour votre aide.