Inscription / Connexion Nouveau Sujet
équilibre d'un solide
bonjour,
Je suis une mamie qui a besoin d'aide...
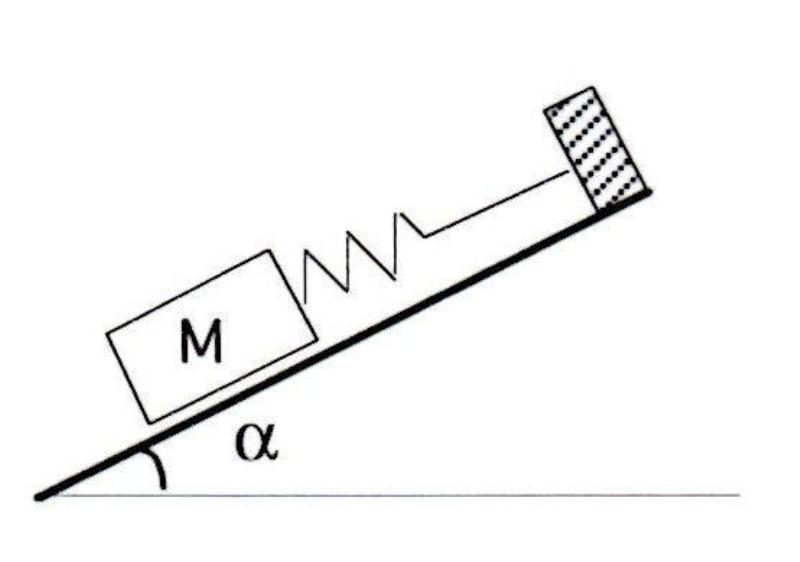
Le ressort qui "retient" l'objet a une raideur k=1N/cm. Sa longueur à vide est de 20 cm. L'objet M peut glisser sans frottement sur le plan incliné( 30°)
30°)
On accroche l'objet a une extrémité du ressort, l'autre étant fixe.
A l'équilibre, la longueur du ressort est de 25 cm.
4-1 Calculer la masse de l'objet. (g= 9,8N/kg)
J'ai calculé:
Calcul de l'intensité de la tension .
La raideur es k=1N/cm
On a la longueur à vide = 20 cm
L'allongement est = delta= 5cm
L'intensité de la tension du ressort est donné par: T = 1*5 = 5
Soit T= 5N
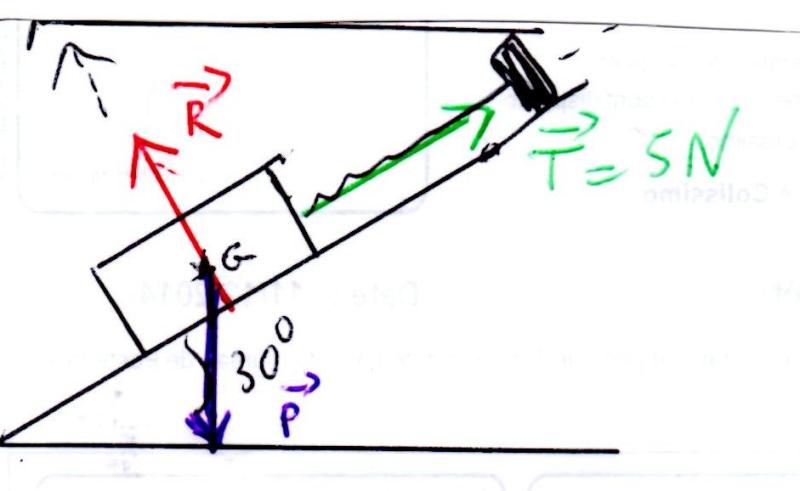
3 forces s'exercent sur ce solide:
le poids vecP, la réaction vecR( perpendiculaire du support en l'absence de frottement) et la tension du ressort dont la droite d'action ses confond avec le ressort.
On peut écrire vecP +vecR +vecT = vec0
Je sais comment trouver m (m=P/g), mais c'est trouver P qui me bloque.
Bonjour fanfan56
"On peut écrire" : en appliquant la première loi de Newton, parce que le solide est immobile, la somme des forces (somme vectorielle) qui s'exerce sur lui est nulle.
Cette somme :
peut être projetée sur l'axe qui nous arrange le mieux.
Un axe parallèle au support (et donc colinéaire avec la tension du ressort) semble tout indiqué.
. se projette en vraie grandeur
. a une composante nulle
. n'est pas difficile à projeter...
En écrivant que la somme des projections est nulle (puisque la projection de est évidemment nulle) on en déduit la valeur de
À toi !

C'est une séquence par rapport aux autres où j'ai du mal à comprendre.
Je ne sais pas si il y a quelque chose de juste dans ce que je vais écrire:
P=T*sin 30°
30°
P=5*sin30°
P= 5/2
Premièrement, indispensable révision de trigonométrie :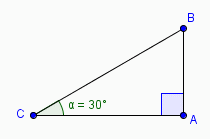
Le triangle ABC est rectangle en A
BC est l'hypoténuse
La mesure de l'angle vaut 30°
Alors la longueur du côté AB vaut BC sin(
sin( )
)
Pour ce cas particulier où  = 30°, le triangle est un demi-triangle équilatéral, si bien que AB = BC / 2
= 30°, le triangle est un demi-triangle équilatéral, si bien que AB = BC / 2
Ou encore... sin(30°) = 0,5
_____________
Le schéma :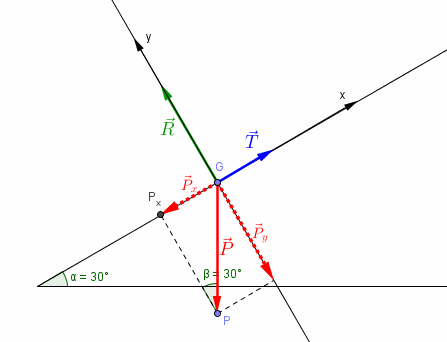
G est le centre de gravité du solide
Gx est un axe parallèle au support et orienté vers le haut (ce qui n'a pas d'importance)
Gy est un axe perpendiculaire au support représente le poids
représente la tension du ressort
représente la réaction du support
La première loi de Newton permet d'écrire (il n'y a pas de mouvement dans un repère terrestre supposé galiléen) : (1)
Le vecteur se projette
. sur l'axe Gx selon
. sur l'axe Gy selon
Si bien que l'égalité vectorielle (1) se projette sur l'axe Gx selon
Dans le triangle GPxP rectangle en Px on a GPx = GP sin(
sin( )
)
Mais  =
=  = 30° (deux angles dont les côtés sont deux à deux perpendiculaires), si bien que
= 30° (deux angles dont les côtés sont deux à deux perpendiculaires), si bien que
GPx = GP / 2
En notant l'intensité du poids il vient :
T - (P/2) = 0
P = 2.T
Puisque
P = 10 newtons
Merci Coll, là ça a le mérite d'être clair.
C'est ce que je reproche à mes cours, pas assez de clarté pour moi.
Donc m=P*g
Soit m = 10*9,8 = 98
La masse de l'objet est 98 kg.

P = m.g
m = P/g
m = 10 / 9,8  1,02 kg
1,02 kg
Qu'il est probablement judicieux d'arrondir à m  1 kg étant données les conditions expérimentales.
1 kg étant données les conditions expérimentales.

Quelqu'un a dit qu'on ne devrait jamais faire un calcul dont on ne connaîtrait pas le résultat par avance. Il y a du vrai...
Or une masse d'un kilogramme a, sur Terre, un poids dont l'intensité est proche de 10 newtons.
____________
Je t'en prie et à une prochaine fois !

Avant de passer à la 2e question
4-2 Calculer la réaction du support.
J'aimerai un peu plus de précisions pour la dernière partie de ton explication, je ne saisis pas très bien
Dans le triangle GPxP rectangle en Px on a GPx = GPsin()
Mais = = 30° (deux angles dont les côtés sont deux à deux perpendiculaires), si bien que
GPx = GP / 2
En notant l'intensité du poids P\ =\ ||\vec{P}|| il vient :
T - (P/2) = 0
P = 2.T
Je veux bien expliquer, mais quoi ?
Il faut me poser des questions claires. Quelle est la ligne que tu ne comprends pas ?

En fait je comprends, mais je n'arrive pas à le rédiger correctement, si tu peux me guider.
[quoteGPx = GP / 2
En notant l'intensité du poids P\ =\ ||\vec{P}|| il vient :
T - (P/2) = 0 ]
(1)
Coordonnée de selon l'axe Gx (orienté vers le haut) : T
Coordonnée de selon l'axe Gx : 0
Coordonnée de selon l'axe Gx (orienté vers le haut) : - P.sin(30°) = - P/2
donc :
T + 0 - (P/2) = 0
d'où
P = 2.T
Mais oui ! 
Cela prouve que tu as compris.
On part toujours de cette même égalité vectorielle (merci la première loi de Newton ! )
(1)
Et cette fois-ci on projette sur l'axe Gy que j'ai orienté vers le haut (mais cela n'a aucune influence sur le résultat final)
Les projections conduisent aux coordonnées suivantes :
. coordonnée de = 0 puisque ce vecteur est perpendiculaire à l'axe Gy
. coordonnée de = R, la valeur inconnue, puisque ce vecteur est parallèle à l'axe Gy
. coordonnée de = - m.g.cos(
 ) puisque la composante de ce vecteur sur l'axe est orientée dans le sens opposé à celui de l'axe. Et la mesure du module de la composante
) puisque la composante de ce vecteur sur l'axe est orientée dans le sens opposé à celui de l'axe. Et la mesure du module de la composante se calcule dans le triangle rectangle.
Donc :
0 + R - m.g.cos( ) = 0
) = 0
R = m.g.cos(30°)
R = 10  cos(30°)
cos(30°)  8,66 N
8,66 N
Qu'il est judicieux d'arrondir à 8,7 N je pense

Bonjour Coll et merci pour ton aide
si tu veux bien je vais récapituler:
Calcul de l'intensité de la tension .
La raideur es k=1N/cm
On a la longueur à vide = 20 cm
L'allongement est = delta= 5cm
L'intensité de la tension du ressort est donné par: T = 1*5 = 5
Soit T= 5N
3 forces s'exercent sur ce solide:
le poids vecP, la réaction vecR( perpendiculaire du support en l'absence de frottement) et la tension du ressort dont la droite d'action ses confond avec le ressort.
On peut écrire la première loi de Newton: vecP +vecR +vecT = vec0
Le vecteur P se projette
. sur l'axe Gx selon vecP_x
. sur l'axe Gy selon vecP_y
Donc l'égalité vectorielle se projette sur l'axe GX
vecT + vec0 + vecPx = vec0
Dont T+0 - (P/2) = 0 ( cette partie m'échappe encore)
d'où P= 2*T
puisque T = 5 N donc 2*T = 10N
P= 10 newtons
selon la formule: m = P/g
m = 10 / 9,8 1,02 kg
Donc m  1kg.
1kg.
4-2 Calculer la réaction du support.
la première loi de Newton:
l'égalité vectorielle se projette sur l'axe Gy
vecT + vec0 + vecPx = vec0
coordonnée de \vec{T} = 0 puisque ce vecteur est perpendiculaire à l'axe Gy
. coordonnée de \vec{R} = R, la valeur inconnue, puisque ce vecteur est parallèle à l'axe Gy
. coordonnée de \vec{P} = - m.g.cos() puisque la composante de ce vecteur sur l'axe est orientée dans le sens opposé à celui de l'axe.
Donc :
0 + R - m.g.cos() = 0
R = m.g.cos(30°)
R = 10 cos(30°) 8,66 N
la réaction du support est  8,7N
8,7N
Est-ce bien rédigé ainsi?
Oui, la rédaction est correcte.
__________
Je ne sais pas comment t'expliquer ce qui t'échappe encore.
Cette égalité vectorielle signifie que la somme des trois vecteurs du premier membre (à gauche du signe = ) est nulle.
En projetant ces trois vecteurs sur un axe quelconque, la somme des trois projections sera encore nulle.
On choisit l'axe pour qu'il nous arrange.
Sont très commodes :
. les axes parallèles à un vecteur, parce que le vecteur s'y projette en vraie grandeur (inutile de faire intervenir un sinus ou un cosinus. Ou encore il faut faire intervenir le cosinus de 0° qui vaut 1... donc, on retrouve la vraie grandeur)
. les axes perpendiculaires à un vecteur, parce que le vecteur s'y projette selon un vecteur nul (et cette fois, c'est comme si on multipliait par le cosinus de 90° qui vaut 0...)
. pour tout autre axe il faudra multiplier la longueur du vecteur à projeter par le cosinus de l'angle entre le vecteur et l'axe pour avoir la longueur du vecteur projeté.
Pour trouver la valeur de j'ai utilisé l'axe Gx
. il est perpendiculaire à dont je ne connais pas encore à ce stade la valeur du module
: la projection de
sur l'axe Gx sera nulle, j'élimine ainsi cette inconnue.
. il est parallèle à qui se projettera donc en vraie grandeur
. il n'y aura qu'un seul vecteur à projeter, ce qui est facile puisque je connais l'angle entre l'axe et le vecteur : 120° (et je n'oublie pas que cos(120°) = -sin(30°) = -1/2 = -0,5 ce qui rend les calculs fort simples)
Je t'introduis ici la mesure de l'angle 120° : c'est une autre manière de considérer que la composante du vecteur
selon l'axe Gx sera orientée en sens inverse de l'axe.
Tu peux donc utiliser (en t'aidant de la figure) soit cos(60°) = sin(30°) = 1/2 puis en prenant l'opposé : - 0,5
soit utiliser cos(120°) = -sin(30°) = -0,5
_________
Sur Gx :
module de la projection de : T
module de la projection de : 0
module de la projection de : -0,5
 P
P
Projection de l'égalité vectorielle
T + 0 - 0,5 P = 0
P = 0
et donc
T = 0,5 P
P
P = T / 0,5 = 2 T
T

Merci Coll,
Alors là j'ai très bien compris, toutes mes questions se sont éclaircies d'un coup encore merci!: :)
:) :)
:) :)
:)
Il me reste un exercice à faire.



