Inscription / Connexion Nouveau Sujet
Oui, Ty = T.cos( )
)
Donc Tx = T.sin(35°)  4 816,6
4 816,6  sin(35°)
sin(35°)  2 762,7 N
2 762,7 N
et
Ty = T.cos(35°)  4 816,6
4 816,6  cos(35°)
cos(35°)  3 945,5 N
3 945,5 N
L'égalité vectorielle :
permet donc d'écrire les égalités suivantes pour les coordonnées :
en projection sur un axe horizontal :
et en projection sur un axe vertical :
On possède les valeurs suivantes :
D'où l'on déduit maintenant les coordonnées de et donc aussi le module
ainsi que l'orientation de cette réaction de l'axe.

Bonjour Coll,
vec Rx + vec0+ vec T = vec0
vec Rx + vec0+ vec2762,7 = vec0
vec Rx + 2762,7 = vec0
vec Rx = -2762,7 N
vec R + vecPy + vec Ty = vec0
vec R + (-11760) + vec 3945,5= vec0
vec R -11760 + vec 3945,5 = vec0
vec R -7814,5 = vec0
vec R = 7814,5 N
Bonjour fanfan56
C'est bon !
Attention quand même : ce n'est pas R mais c'est Ry qui est la coordonnée du vecteur sur l'axe Oy
Ce n'est pas non plus, comme tu l'écris, vec Rx = - 2 762,7 N
Mais c'est Rx qui est la coordonnée du vecteur sur l'axe Ox et qui vaut - 2 762,7 N
____________
L'énoncé demande l'intensité de cette réaction de l'axe
Tu connais donc :
Rx = - 2 762,7 N
Ry = + 7 814,5 N
Tu peux donc facilement calculer le module du vecteur qui s'écrit, au choix,
ou
Je te ferai ensuite une rédaction de la solution pour ce long topic. Tu verras que c'est beaucoup plus simple que l'opinion que tu t'en fais probablement à l'heure actuelle.

On peut peut-être utiliser Pythagore?
J'ai pris comme exemple les coordonnées de vecT
Tx² + Ty² = T
2762,7²+ 3945,5² = 4816,58
et Rx² +Ry² = -2762,7² + 7814,5² = 7309,85
Mais il doit sûrement y avoir une autre méthode?
Bien sûr qu'il faut utiliser Pythagore. Mais... horreur !
Rx2 + Ry2 = (- 2 762,7)2 + (7 814,5)2 = ... ?
__________
Ceci est très mal écrit :
2762,7²+ 3945,5² = 4816,58
Parce qu'il est évident qu'il aurait fallu écrire :
2762,7²+ 3945,5² = 4816,58²
Donc que vaut R ? (qui ne peut quand même pas être plus petit que Ry... )
Il faut toujours vérifier la plausibilité des résultats que l'on annonce.

Exact.
_____________________
On suppose que le pont est immobile.
Deux conditions sont nécessaires pour qu'il en soit ainsi :
(1) La somme des moments des forces appliquées par rapport à un axe quelconque doit être nulle
(2) La somme des forces extérieures appliquées doit être nulle
Un schéma :
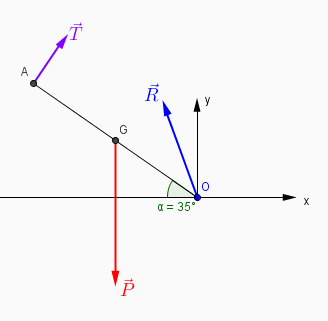
(1) Première condition : nullité de la somme des moments par rapport à un axe quelconque
On choisit comme axe l'axe de rotation passant par O
On choisit comme sens positif des rotations le sens direct
Moment de : P.OG.cos(
 )
)
Moment de : -T.OA
Moment de : 0 puisque cette force passe par l'axe choisi (ce qui justifie ce choix)
P.OG.cos( ) - T.OA = 0
) - T.OA = 0
T = P.OG.cos( )/OA
)/OA
Application numérique :
T = 1 200  9,8
9,8  4
4  cos(35°) / 8
cos(35°) / 8  4 816 N
4 816 N
(2) Deuxième condition : nullité de la somme des forces appliquées
Il faut donc que
On choisit un repère :
Origine O
Axe Ox : horizontal
Axe Oy : vertical
Dans ce repère la condition précédente s'écrit, par projection sur les axes :
On connaît et
, donc :
et
d'où :
D'où la valeur de la réaction de l'axe
On pourrait aussi en déduire l'orientation de cette réaction de l'axe : l'angle entre le vecteur unitaire porté par l'axe Ox et le vecteur vaut environ 109,5°
Pour information : la figure que j'ai postée est à l'échelle et les mesures des angles y sont respectées.

Merci Coll et surtout de ta très grande patience!!!
Je vais pouvoir envoyer ce devoir dès demain.
Ensuite je laisse un peu la physique pour me remettre aux maths ( vecteurs encore.... et produits scalaires) A très bientôt j'espère...
Oui, les vecteurs sont un outil indispensable en physique.
Et, pour les "manipuler" dans des expressions mathématiques, il faut avoir compris ce que sont les composantes d'un vecteur (d'autres vecteurs dont la somme est égale au vecteur ainsi "décomposé") et ce que sont les coordonnées d'un vecteur sur un axe (que l'on obtient par un produit scalaire).
____________
Je t'en prie.
Bon courage pour les mathématiques et à une prochaine fois !



