Niveau terminale

Equations horaires et vecteurs positions

Posté par
chimchon 03-06-14 à 01:16

Bonjour,

je suis nouveau dans le site, et je suis en terminale S. Je suis sur le chapitre de la dynamique newtonienne et je comprend que très difficilement le cours. Je me suis lancé sur un exercice que j'ai beaucoup de mal a comprendre, c'est pourquoi je demande votre aide.

Voici l'exercice: ** lien vers l'énoncé effacé **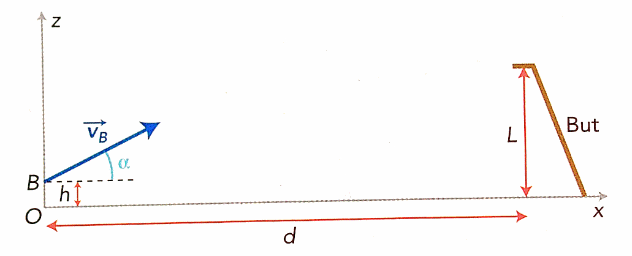

Equations horaires et vecteurs positions

Je commence:

1) Le système étudiée est le mouvement de la balle dans un référentiel supposé galiléen.
Coordonnée du vecteur VB a t=0s

vecteur VB|VBx=V0cosa
          |VBy=Vosina

1re question: je sais que c'est le cours, mais je comprend pas pourquoi VBx= V0cosa et VBy=V0sina.
Autrement dit, ici sur l'exo, je le fais sans comprendre.
2eme question: doit-on cité ou pas la loi de newton ? Et pourquoi ?

2) Les coordonnées XB et ZB du vecteur position OG de la balle au point B sont :

Vecteur OG|X=0
          |z=h

3) Donc ici, d'après la loi de newton on sait que vecteur a= vecteur g

vecteur a|ax =??
         |az = ??
Je sèche. J'ai aussi une autre question ici. Quand on enlève les vecteurs, ça fait a=-g ?

Je ne peux plus continuer l'exercice car je n'ai pas répondu a la 3), c'est pourquoi, j'attend au plus vite vos réponses en étant le plus clair possible svp.

Merci d'avance de votre aide.

Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum
Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !

Posté par re : Equations horaires et vecteurs positions 03-06-14 à 01:29

J'ai oublié de précisé que c'était le 1er exercice que je fais dans le lien que j'ai inscris.

Posté par re : Equations horaires et vecteurs positions 03-06-14 à 10:51

D'accore je comprend. Voici l'énoncé de l'exercice alors:

Pratiqué depuis l'Antiquité sous le nom de « jeu de crosse », le hockey sur gazon est un sport
olympique depuis 1908. Il se pratique sur une pelouse naturelle ou synthétique, de dimensions
quasi identiques à celles d'un terrain de football. Chaque joueur propulse la balle avec une
crosse, l'objectif étant d'envoyer la balle dans le but adverse.

Dans cet exercice, on étudie le mouvement du centre de la balle de masse m, dans un
référentiel terrestre supposé galiléen.
À la date t = 0, la balle quitte la crosse au point B avec le vecteur vitesse ⃗ ⃗⃗⃗ contenu dans le
plan (xOz) comme le montre le schéma.
On néglige toutes les actions dues à l'air. Le mouvement du centre de la balle est étudié dans
le champ de pesanteur supposé uniforme.
Le système d'axes utilisé est représenté sur le schéma ci-dessous : l'axe (Ox) est horizontal
dirigé vers la droite, l'axe (Oz) est vertical et dirigé vers le haut. L'origine des axes est située à
la verticale du point B telle que OB = h = 0,40 m

-image zur le post1-

1. Exprimer les coordonnées vBx et vBy du vecteur vitesse ⃗⃗⃗⃗ du centre G de la balle à
l'instant t = 0 s, en fonction de vB et de .
2. Quelles sont les coordonnées xB et zB du vecteur position OG de la balle au point B ?
3. Déterminer les coordonnées ax et ay du vecteur accélération de la balle au cours du
mouvement.
4. En déduire les coordonnées vx(t) et vy(t) du vecteur vitesse du centre G de la balle.
5. Déterminer les coordonnées x(t) et y(t) du vecteur position OG du centre G de la balle.
6. En déduire l'équation de la trajectoire du point G.
7. La ligne de but est située à une distance d = 15,0 m du point O. La hauteur du but est
L = 2,14 m. On néglige le diamètre de la balle devant la hauteur du but.
Le but est-il marqué?

Voila. J'espere maintenant recevoir une réponse le plus vite possible.

Posté par re : Equations horaires et vecteurs positions 03-06-14 à 12:06

Bonjour,

Les notations sont un peu confuses...

Je note $\vec{v}(t)$ le vecteur vitesse en fonction de t

La balle est au point B à l'instant t = 0
Je note donc la vitesse initiale $\vec{v}(0)$ qui est $\vec{v}_B$ du schéma.
En notant $v_B\,=\,||\vec{v}(0)||$ la norme de cette vitesse initiale comme le demande l'énoncé.

Par projection sur les axes Ox et Oz les composantes (ou "coordonnées") du vecteur vitesse initiale sont donc :

$\vec{v}_B\,=\,\vec{v}(0)\;\left \lbrace \begin{array}{c} v_{Bx}\,=\,v_B.cos(\alpha) \\ v_{Bz}\,=\,v_B.sin(\alpha) \end{array}$

Comprends-tu cela ?

Posté par re : Equations horaires et vecteurs positions 03-06-14 à 16:34

En notant v_B\,=\,||\vec{v}(0)|| la norme de cette vitesse initiale comme le demande l'énoncé.

Ou vous voyez cela ? Et qu'est-ce que cela change de l'écrire de cette façon ?

Sinon j'ai compris le reste, mais encore une fois, j'ai une question de cours pourquoi VBx= VBcosa et VBz=Vbsina. Ce que je veux dire, c'est d'ou vient le cos et le sin ? c'est cosa=opposé/adjacent, c'est ça la formule ou c'est pas du tout ca ?

Ps: dsl mais je sais pas écrire les vecteurs sur l'ordi.

Posté par re : Equations horaires et vecteurs positions 03-06-14 à 16:35

petite erreur, c'est cosa=adjacent/hypoténuse.

Posté par re : Equations horaires et vecteurs positions 03-06-14 à 19:35

Tu as appris comment trouver les composantes d'un vecteur parallèles à différentes directions. Et tu as aussi appris à trouver les coordonnées d'un vecteur sur des axes.

Soit et les vecteurs unitaires sur les axes Ox et Oz

On trouve les coordonnées (des nombres, des scalaires...) du vecteur $\vec{v}_B$ sur chaque axe en faisant les produits scalaires

$v_{Bx}\,=\,\vec{v}_B.\vec{i}\,=\,v_B.\cos(\alpha)$
et
$v_{Bz}\,=\,\vec{v}_B.\vec{k}\,=\,v_B.\cos(\dfrac{\pi}{2}\,-\,\alpha)\,=\,v_B.\sin(\alpha)$

Les composantes du vecteur $\vec{v}_B$ parallèles aux axes Ox et Oz sont donc respectivement $v_B.\cos(\alpha).\vec{i}$ et $v_B.\sin(\alpha).\vec{k}$
__________

Question 2

$\vec{OG}(0)\,=\,\vec{OB}\; \left \lbrace \begin{array}{c} x_B\,=\,0 \\ z_B\,=\,h \end{array}$
__________

Question 3

Pendant le mouvement la balle n'est soumise qu'à une seule force : son poids.
D'après la deuxième loi de Newton, son accélération est donc

$\vec{a}\,=\,\vec{g}\; \left \lbrace \begin{array}{c} a_x\,=\,0 \\ a_z\,=\,-g \end{array}$

En notant g la norme du vecteur champ de pesanteur : $g\,=\,||\vec{g}||$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Equations horaires et vecteurs positions

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique