Inscription / Connexion Nouveau Sujet
équations de trajectoire
Bonjour,
Sur cet exercice je suis face à un mur :
Pour étrenner son are flambant neuf, Ruben va dans un parc et vise un écureuil sur une branche à une hauteur à du sol et à une distance horizontale d. A l'instant précis où la flèche part, avec une vitesse initiale v0 l'écureuil se laisse tomber.
Dans tout l'exercice, on néglige les frottements.
1) En notant les coordonnées avec un indice "e" pour l'écureuil et "f" pour la flèche, établir pour les deux mouvements les équations horaires et l'équation de la trajectoire.
2) Montrer que si la chute verticale de l'écureuil ne prenait jamais fin, il serait touché par la flèche quelle que soit v0.
3) En déduire que l'écureuil ne pourra échapper à la flèche que si vo est inférieure à une vitesse v1 qu'il faudra déterminer.
4) Calculer la valeur numérique de v1 avec h = 10 met d = 50 m.
Il s'agit donc bien d'exprimer les deux trajectoires dans le même repère pour les étudier mais l'on ne nous donne pas la taille de l'archer. Je ne vois donc pas comment placer mon repère.
Quand bien même je la supposerai (ce que j'ai tenter de faire), je n'ai pas l'angle au quel est tiré la flèche...
Fin bref je pense que quelque chose m'échappe dans la résolution de l'exercice, que me conseiller vous pour cet exercice ?
Merci d'avance
Bonjour
Commence par faire un schéma précis. Tu peux écrire les équations horaires des deux mouvements. Que peut-on dire des deux altitudes ?
Un schéma est-il fourni avec l'énoncé ? Si oui, peux-tu le scanner et le poster ici.
Sinon, on peut sans doute interpréter l'énoncé de la façon suivante :
Noter he la hauteur initiale de la flèche et considérer que "viser l'écureuil" consiste à donner une vitesse initiale orientée de la position initiale de la flèche vers la position initiale de l'écureuil. l'angle entre l'horizontale et le vecteur vitesse initiale est ainsi facile à exprimer à partir de sa tangente.
Merci beaucoup pour votre aide, non pas de schéma. Voici comment avance mes recherches à l'aide de vos conseils :
1) On note (xe ; ze) et (xf; zf) les coordonnées de l'écureuil et la flèche. On se place dans un repère ayant pour origine O l'archer. Avec
xe(0) = d et ze(0) = h et xf = 0
2e loi de Newton : (->g) = (->a) (déolé je ne trouve pas comment faire des vecteurs, j'espère que ça restera lisible
J'aboutit pour les équations horaires à : (->OF) :
xf(t) = v0* cos
* t
yf(t) = 0
zf(t) = (-1/2)*g*t^2 + v0*sin * t + zf(0)
Et (->OE) : xe(t) = d
ye(t) = 0
ze(t) = (1/2)*g*t^2 + h
Et pour les équations de trajectoire :
- Pour la flèche : zf(xf) = (-g / (2* v0^2 * (cos)^2)) * xf^2(t) + tan * xf(t) + zf(0)
- Pour l'écureuil : xe(t) = d (z ne dépendant pas de x, et une equation horaire étant sans t (?), cela revient à cette équation ?)
Si j'ai bien compris votre remarque, je peux trouver l'angle par :
tan = (h-zf(0)) / d
= tan^-1((h-zf(0)) / d)
Pour la question 2) :
Je comprend qu'il faut exprimer zf(d) = ze(t)
Et me retrouve donc avec t = racine d'un truc gigantesque dont je ne vois pas comment je peux prouver que c'est positif et donc que un t existe.
A savoir, je dois avoir tan()*d + zf(0) -h > (g)/(2* v0^2 * cos^2())*d^2
Je bloque donc encore, mais des avancées ont l'air d'avoir été faite 
Qu'en pensez vous ?
mais des avancées ont l'air d'avoir été faite
Oui bien sûr !
Tes équations horaires et les équations de trajectoires sont bonnes. Je note pour simplifier : ho=zf(0).
Il me me paraît pas nécessaire d'étudier en détail la trajectoire de la flèche. Bien sûr ici, la flèche et l'écureuil sont assimilés à ces points matériels.
Pour la question 2 :
Étape 1 : si la flèche atteint l'écureuil, cela se produit à une date t1 telle que xe(t1)=xf(t1)
Étape 2 : la flèche atteint l'écureuil à la date t1 si :
ze(t1)-zf(t1)=0
Calcule donc cette différence d'altitude ; en tenant compte de la valeur de tan(
) tu vas obtenir la valeur de la différence d'altitude attendue.
Étape 3 : Bien entendu, l'étude précédente n'est valide que pendant la chute de l'écureuil entre la branche et le sol. Cela implique :
ze(t1)>0 ; l'écureuil ne s'enfonce pas dans le sol. De l'inégalité sur t1 qui en résulte, on peut obtenir une inégalité vérifiée par v1. C'est là que l'énoncé manque de rigueur. L'inégalité fait intervenir g, d, h mais aussi ho...
Et choisir ho=0 n'est pas réaliste...
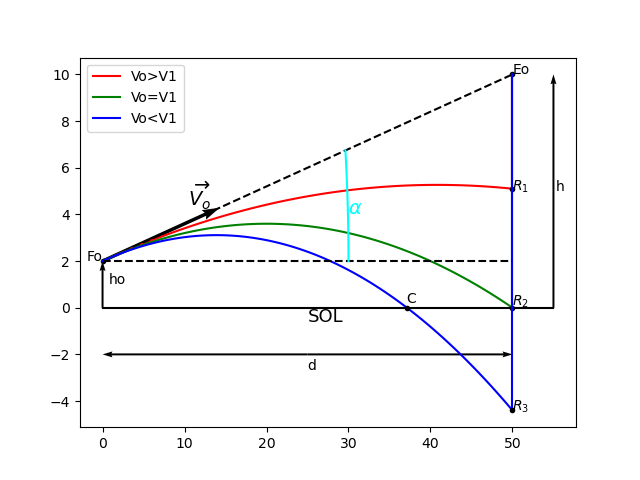
Voici une simulation pour illustrer mon message précédent. Trois cas sont envisageables pour une même valeur de ; (Fo est la position initiale de la flèche, Eo la position initiale de l'écureuil) :
1° : (en rouge) Vo>V1 : la flèche perce l'écureuil en R1.
2° : (en vert) Vo=V1 : cas limite où la flèche perce l'écureuil en R2 juste comme l'écureuil arrive au sol.
3° : (en bleu) Vo<V1 : la flèche n'a pas assez de vitesse initiale pour atteindre la trajectoire verticale de l'écureuil. Elle se plante dans le sol en C. R3 représente le point de rencontre théorique déterminé à la question 2. Ce point est à l'intérieur du sol et bien sûr, ne peut pas être atteint !
Annuler
connectez vous