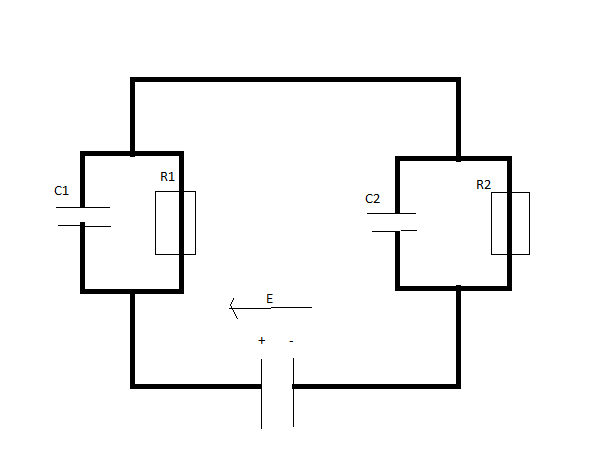
Bonsoir
Un peu difficile en terminale... il faut commencer par orienter le circuit et préciser la signification de q1 : charge de quelle armature.
Que proposes tu comme éléments de réflexion  et début de solution  ?

j'ai un brouillon d'idées dans la tête
voici une proposition:
C1 et C2 sont montés parallèlement
C1+C2=Ce
de même pour R1 et R2 on trouve Re=R1R2/(R1+R2)
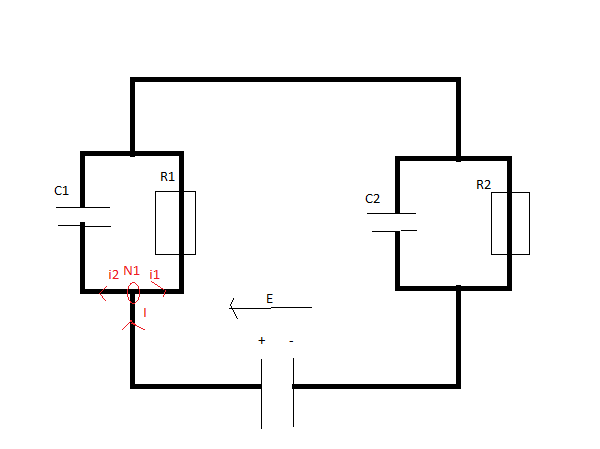
ensuite dans le noeud N1 (doc en bas)
I=i1+i2
E/Re=Ur1/R1+dC1Uc1/dt
je m'arrête ici parce que je ne sais pas si ceci va me mener quelque part
2e proposition
dans la maille 1
Uc1+Ur1=0
q1/C1+R1i=0
q1/C1+R1dq1/dt=0

Tu est bien certain du schéma du montage  ?
Si Oui, R1 est en parallèle avec C1 et R2 est en parallèle avec C2 et l'association (R1//C1) est en série avec l'association (R2//C2). Celà n'est pas simple au niveau terminale.  Il s'agit d'un exercice donné par ton professeur ou d'un exercice trouvé dans un livre ? As-tu déjà étudié la charge d'un seul condensateur en série avec une résistance  ?

il s'agit bien d'un exercice donné par mon professeur.
concernant la charge d'un seul condensateur en série avec une résistance, parlez-vous du cas où l'on charge le condensateur par un générateur de tension et qu'il est monté en série avec une résistance (là où la somme Ur+Uc=E en général)? si oui j'ai déjà étudié ceci.

Il faut tenir compte de R2 et C2 et bien préciser sur le schéma q1 et la charge q2 du deuxième condensateur.  Écrire ensuite les différentes lois que tu connais puis simplifier...

Pour t'aider un peu : voici un schéma annoté. J'ai ajouté un interrupteur (K) : je suppose que celui-ci se ferme à la date t=0 alors que les deux condensateurs sont déchargés.

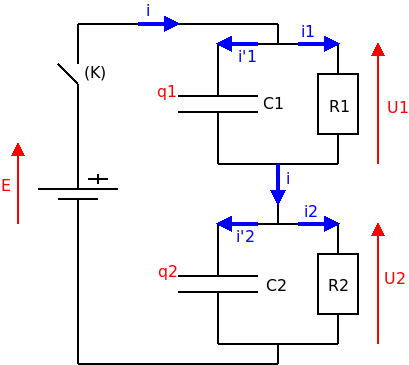
merci pour votre schéma!
I=i1+i'1
=U1/R1+dq1/dt
I=i2+i'2
=U2/R2+dq2/dt

U1/R1+dq1/dt=U2/R2+dq2/dt
q11/(C1R1) + dq1/dt= q21/C2R2+dq2/dt

Ce que tu as fait est tout à fait correct !
Pour terminer, il faut éliminer q2 et dq2/dt. Cela peut se faire en remarquant :



Expression que tu peux aussi dériver par rapport au temps sachant que E est une constante.

sinon peut-on dire que les résistances sont en série et que I=E/(R1+R2)?

je viens de voir votre réponse
je vais ajouter votre expression à ma réponse

on obtient alors:
0=dU1+dU2=d(q1/C1)/dt +d(q2/C2)/dt
(1/C1)dq1/dt+(1/C2)dq2/dt=0
C2((-1/C1)dq1/dt)=dq2/dt

(-C2/C1)dq1/dt=dq2/dt
on remplace dans l'équation de toute à l'heure
q11/(C1R1)+dq1/dt = (U2/R2) -(C2/C1)dq1/dt
q11/(C1R1) +dq1/dt (1+C2/C1) =U2/R2

Tu y es presque : il faut aussi faire disparaître u₂ de l'équation :

q11/C1R1 + (dq1/dt)(1+C2/C1)=(E-q1/C1)/R2
                                                                                                                     =E/R2 - q1/C1R2
q1/C1R1 + q1/C1R2  + (dq1/dt)(1+C2/C1)=E/R2
q1(1/C1R1 + 1/C1R2) + dq1/dt (1+C2/C1)=E/R2
q1(1/C1) (1/R1 +1/R2) + dq1/dt (1+C2/C1) =E/R2
?

Très bien : ton résultat est correct ! Il y a possibilité de le simplifier un peu pour faire apparaître une constante de temps et mettre en évidence le comportement asymptotique de q₁, c'est à dire la valeur de q₁ en fin de charge. Pour cela, on introduit la résistance R_e équivalente à l'association en parallèle de R₁ et R₂ :



On multiplie tous les termes de ton équation par :

Cela donne :



Cela est une équation différentielle du premier ordre de la forme :



avec :

: constante de temps ;

: valeur limite de q₁ quand t tend vers l'infini, la charge étant ainsi terminée.

tout est clair, je vous remercie énormément!

J'ai commis une étourderie d'exposant ; je rectifie :

Heureusement, il s'agit juste d'une étourderie de copie sous l'éditeur d'équations. Cela n'affecte pas les autres équations et le résultat.

Oui je l avais remarqué toute à l'heure
J ai oublié de vous le signaler
Bonne soirée!