Inscription / Connexion Nouveau Sujet
équation différencielle d une charge
Bonjour tout le monde,
J'aimerais à nouveau vous soumettre mon travail, parce que je continue à ne pas être extrèmement à l'aise.
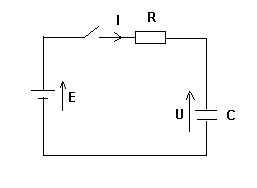
On réalise la charge d'un condensateur de capacité C= 10
F. Dans l'ordre on a un générateur (alim stabilisée) E=12V, un conducteur ohmique (Uab) R= 1Okohm, et un condensateur (Ubd). Le condensateur est déchargé et on ferme l'interrupteur K (qui était fermé jusque là 
).
1) Soit qb=q la charge de l'armature B du condensateur. i= dq/dt. Indiquer l'orientation du courant i(t).
de A vers B
2) On pose Ubd=u. Exprimer la tension Uab en fonction de u et des éléments du circuit.
Uab= E-u
3) Trouver l'équation différentielle vérifiée par u(t)
E= Uab+ u
Uab=R.i= R.dqb/dt= RC.dUbd/dt
E= RC.dUbd/dt +u
4) Cette équation diff admet une solution de la forme
u(t)= A(1- exp(-t/
)
a) Déterminer les expressions littérales de A et
Dans mon bouquin, j'ai un exo corrigé du même genre dont je ne comprends pas la correction. On me dit que pour t=0, u=E ce qui me paraît absurde puisque le condensateur n'est pas chargé... Et la conclusion est u(t=0)=A=E
Je ne sais pas trop comment démontrer que E=A et que tau=RC
b)E=12 et tau= RC= 0,1 s
c)exprimer l'intensité de charge i(t)
i(t)= dqb/dt= Cdu/dt et i(t)=Uab/R
5) Exprimer littéralement à l'instant t=0s puis calculer u, du/dt, i, et di/dt
u= qb/C= it/c =0
i= dq/dt= Cdu/dt
du(0)/dt= i(0)/C= Uab(0)/RC= 120 V (je suppose qu'on parle de tension instantanée)
i=Uab/R= 1,2 mA
di/dt Là je ne vois pas trop. Il va falloir que je finisse demain...
Je continue...
di/dt= C d(du/dt)/dt et ça ne doit pas être ça...
Ou plutôt:
di/dt= dU/R /dt= 1/R 1/R . dUab/dt= 1/R.d(E-u)/dt= 1/R. dE/dt -1/R.du/dt
= -1/R.du(0)/dt=-1/10.10^3 .120= -0,12.10^-3A= -0,12 mA
6)Déterminer la date
u= E/2
u= E(1- e^(-t/RC)
E/2= E(1- e^(-t/RC)
e^(-t/RC)= 1/2
-t/RC = -ln2
t= RC.ln2
= RC.ln2 =10.10^3.10.10^-6.ln2= 70.10^-3 s= 70 ms
b) A quelles dates a t'on u(t)= E/4? u(t) = E/8?
E/4= E(1- e^(-t/RC)
e^(-t/RC)= 3/4
-t= RC.ln (3/4)
t= -RC.ln3 + RC.ln4= 29.10^-3 s= 29ms
E/8= E(1- e^(-t/RC)
e^(-t/RC)= 7/8
-t= RC.ln (7/8)
t= -RC.ln(7/8)= 13.10^-3s = 13ms
Que de chemins détournés pour un truc simple.
Avec mon dessin, on ferme l'interrupteur au temps t = 0.
E = U + R.I
I = C. dV/dt
E = U + RC.dV/dt
Equation différentielle dont les solutions sont:
U = A.e^(-t/(RC)) + E (avec A une constante à déterminer par les conditions intiales).
En t = 0, on a U = 0 et donc:
0 = A.e^(0) + E
0 = A + E
A = -E
--> U = E(1-e^(-t/(RC))
Avec I = C.dU/dt
I = C.E.(1/RC).e^(-t/RC)
I = (E/R).e^(-t/(RC)
-----
On a donc en regroupant les résultats:
U = E(1 - e^(-t/(RC))
I = (E/R).e^(-t/(RC)
-----
Sauf distraction
Avec I = C.dU/dt
I = C.E.(1/RC).e^(-t/RC)
Tu n'aurais pas oublié le - de 1/RC en dérivant u?
Sinon effectivement c'est beaucoup plus rapide comme ça
J'y penserai à l'avenir.
Non, je n'ai pas oublié le -.
Voila en très fort détaillé:
U = E.(1-e^(-t/(RC))
dU/dt = E.d(1-e^(-t/(RC))/dt
dU/dt = E.d(-e^(-t/(RC))/dt
dU/dt = -E.d(e^(-t/(RC))/dt
dU/dt = -E.(-1/RC).e^(-t/(RC)
dU/dt = (E/RC).e^(-t/(RC)
C.dU/dt = (E/R).e^(-t/(RC)
I = (E/R).e^(-t/(RC)
----
Annuler
connectez vous