Inscription / Connexion Nouveau Sujet
energie potentielle-energie mécanique
Bonjour , j'ai besoin d'aide pour resoudre l'exercice
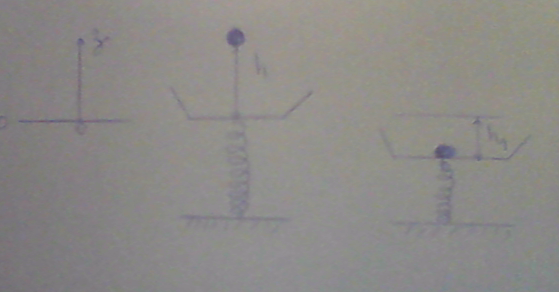
Enoncé: Une bille en plomb de masse m=100g tombe en chute libre d'une hauteur h=1 m sur un plateau de masse négligeable supporté par un ressort vertical .Au moment du choc ,la bille s'immobilise sur un plateau qui s'abaisse d'une hauteur h1= avant de s'osciller. g=10 N/kg
1) Calculer la vitesse de la bille au contact du plateau
2) Sachant que le ressort a pour raideur K=840 N/m,déterminer la hauteur h1 en appliquant le théorème de l'énergie cinétique et le théorème mécanique
bonjour athrun et very
1)je propose :
methode 1: Application du th de Ec on a:
soit A le pt de depart de la bille ,Va=0 et B le pt de contact de la bille avec le plateau Vb=?
?Ec= W(P)?Ec(b)-Ec(a)=mgh?1/2mVb²-0=mgh =>Vb= (2gh)=
(2gh)= (2x102x1)=4.47m/s
(2x102x1)=4.47m/s
methode 2:application de la conservation Em en supposant en chute libre que la resistance du a l'air est négligés Em=0 <=> Em=cste
Em=0 <=> Em=cste Em=0 <=> Em(b)-Em(a)=0
Em=0 <=> Em(b)-Em(a)=0
<=> Em(b)=Em(a)
<=> Ec(b)+Ep(b)=Ec(a)+Ep(a)
or Ep(b)=0 et Ec(a)=0
=> Ec(b)=Ep(a)
<=> 1/2mVb²=mgh
avec h=Za => Vb= (2gh)=
(2gh)= (2x102x1)=4.47m/s
(2x102x1)=4.47m/s
2) En appliquant  Ec :
Ec :
 Ec= W(P) +W(T)
Ec= W(P) +W(T)
<=> Ecf-Eci=mgh1-1/2K?x²
<=> -Eci=mgh1-1/2K.(h1 )²
avec Ecf=0 jarrive pas a continue je n'ai bien compris
Bonjour,
Ok pour la question 1. Pour la question 2 on considère le système {bille + plateau + ressort}. Le ressort et le plateau ayant une masse négligeable, la masse de ce système est (celle de la bille).
Tu as en effet via le théorème de l'énergie cinétique appliqué à notre système entre l'instant où la bille arrive sur le plateau (instant initial, vitesse , altitude
) et l'instant où le système est à la position la plus basse (instant final, vitesse nulle, altitude
) :
où
(le poids fournit un travail moteur tandis que la force de rappel du ressort fournit un travail résistant).
D'autre part où
est la vitesse déterminée en 1.


