Inscription / Connexion Nouveau Sujet
Énergie mécanique ( vitesse d'une bille et son altitude)
Bonjour
Bonne année 2016
J'aurais besoin d'aide pour cet exercice :
Chapitre : énergie mécanique.
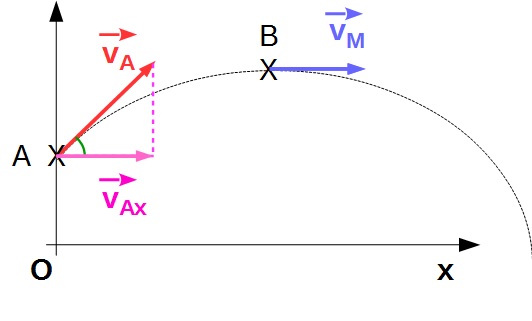
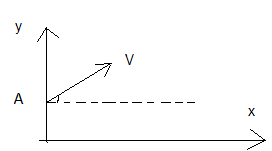
Une bille supposée ponctuelle est lancée d'un point A situé à une hauteur h du sol avec une vitesse VA.
Le vecteur vitesse fait avec le plan horizontal un angle
 .
.
On admettra que la composante du vecteur vitesse suivant l'axe x'x reste constante durant tout le mouvement de la bille.
Trouver la vitesse de la bille à son arrivée au sol.
Trouver l'altitude maximale atteinte par la bille.
On donne  =60° ; h=2 m; VA= 20 m/s; g= 9,8 SI.
=60° ; h=2 m; VA= 20 m/s; g= 9,8 SI.
Merci d'avance
Bonjour.
Le théorème de l'énergie cinétique ou la conservation de l'énergie mécanique permettent d'obtenir la réponse très rapidement.
À vous.
Pourquoi W(P) = - mgh ?
Du point A au point de chute la bille perd de l'altitude, le travail du poids est donc moteur.
Pour éviter ce genre d'erreur, écrivez plutôt :
z désignant l'altitude du centre d'inertie.
Ici : et
on a donc :
Ou bien
L'état de référence: sol
EmA= EcA+EpA
Donc EmC= EcC ==>
1/2.mVc2= 1/2.mVA2+mgh
Vc2= VA+2gh ?
Mais cette expression corrigée est bonne ?
Donc on peut attaquer 2.
Avec la convention:
1/2.mV2Amgh ==>
?
Mais cette expression corrigée est bonne ?
Donc on peut attaquer 2.
Avec la conservation:
1/2.mV2Amgh ==>
Non, ça ne va pas !
En A, l'énergie mécanique est : EmA = 1/2 m vA2 + m g h
Au point M d'altitude maximale, l'énergie mécanique est : EmM = EpM + EcM
L'énergie potentielle s'écrira : EpM = m g zM zM étant l'altitude cherchée.
L'énergie cinétique s'écrira : EpcM = 1/2 m vM2
Que vaut vM ?
Relisez bien l'énoncé.
Non, VM n'est pas nulle.
En M, la bille cesse de monter, mais elle continue son déplacement horizontal vers la droite.
La composante verticale de la vitesse s'annule en M, mais la composante horizontale conserve la même valeur pendant tout le mouvement.
Une erreur de notation m'a échappé dans votre message de 12 h 16.
Ce n'est pas : vMx = vM cos  , mais vMx = vM = vA cos
, mais vMx = vM = vA cos 
Je développe un peu.
On a...
d'une part : vAx = vA cos 
d'autre part : vMx = vM puisque vMy = 0
Comme, d'après l'énoncé...
On admettra que la composante du vecteur vitesse suivant l'axe x'x reste constante durant tout le mouvement de la bille.
on peut écrire que : vMx = vAx
Soit, finalement : vM = vMx = vAx = vA cos

OK ?