Inscription / Connexion Nouveau Sujet
Energie mécanique
Bonjour, j'aimerais que vous m'aider à finir cet exercice:
Une voiture de massse m=800kg gravite une cote de 10% (la dénivellation est de 10 m pour un parcours de 100m) à la vitesse constante V.
1) Calculer la variation de l'énergie mécanique du système terre-voiture pour un parcours de 500m.
g=9,8N/Kg, on prendra que pour d=0 , Ep=0
J'ai trouvé ici Em=392000J.
2)Quelle est la valeur de F (force) de même direction avec le déplacement nécessaire pour augmenter l'énergie mécanique du système terre-voiture sur le même parcours?
C'est là où je me bloque !
Pouvez-vous m'indiquer une piste!?
Bonjour fidele11,
Tu n'es pas nouveau sur le forum, tu sais donc comment on fonctionne.
Où sont tes pistes de réflexion pour les questions déjà résolues ?
Avec un minimum de rédaction, de justifications, un schéma de la situation, etc.
1) pour la première question, la variation de l'énergie mécanique est égale à : Em(final) - Em(initial)
===>(Epf+Ecf)-(Epi+Eci)
===>mgh+½mv²-0-½mv²
===>800*9,8*50=392 000J
2) Pour la 2e question, je pense que je vais utiliser le travail de F:
on sait que W(F)= F*d*cos@
je tire donc F=W(F)/d*cos@
là, je considère que W(F)= 392J.
est ce une bonne voie?
Question 1 : il faut expliquer ce que tu fais avec des mots !
Rappeler par exemple :
- que la voiture a un mouvement rectiligne uniforme => Ecf - Eci = 0
- l'origine du repère est à la position initiale de la voiture => Epi = 0
La voiture monte de 10 m pour 100m parcourus sur la pente, donc elle montera de 50 m pour 500 m parcourus => Epf = énergie potentielle de pesanteur = m*g*h
Finalement, la variation d'énergie mécanique faut  Em = Epf = 800*9,8*50 = 3,92.105 J
Em = Epf = 800*9,8*50 = 3,92.105 J
En effet, il ne faut pas mettre plus de 3 chiffres significatifs à ton résultat ici : ![]() Les chiffres significatifs
Les chiffres significatifs
Question 2 :
Pourquoi peux-tu écrire que ? Sur quelle hypothèse t'appuies-tu ?

Oh désolé, j'avais oublié une donnée de la question 2 :
2)Quelle est la valeur de F (force) de
même direction avec le déplacement
nécessaire pour augmenter l'énergie
mécanique du système terre-voiture de 392 J sur le
même parcours?
Oh désolé, j'avais oublié une donnée de la
question 2 :
2)Quelle est la valeur de F (force) de
même direction avec le déplacement
nécessaire pour augmenter l'énergie
mécanique du système terre-voiture de
392 KJ sur le
même parcours?
J'ai donc pensé qu'augmenter l'energie mécanique de 392KJ signifierait une application d'une force de travail W=392KJ ?
Tu es sûr de l'unité de l'augmentation de l'énergie mécanique ? Cela me paraît un peu faible.
En revanche je ne comprends pas en quoi le cosinus de l'angle interviens : ta force motrice a la même direction que le déplacement, tu l'as écris toi-même !
En revanche, tu as oublié une chose : le poids du véhicule travaille également, c'est un travail résistant et non moteur comme ...

Devrais-je alors apliquer la variation de l'énergie cinétique :
♦Ec=W(P)+W(F)+W(R) ?
Et remplacee dans la relation de ♦Em ?
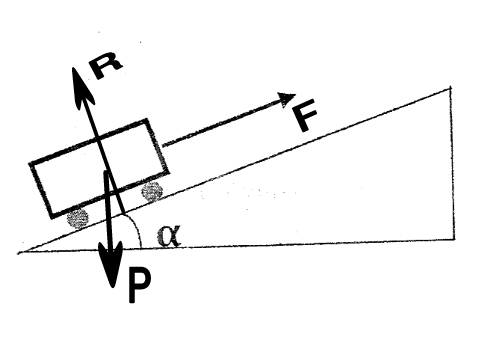
Il manque le repère d'étude sur ton schéma, sinon le représentation des forces est correcte => cependant, tu confirmes que les frottements sont négligeables (ce que ton schéma suppose) ?
Sinon, tu as un bon début de raisonnement ...
Détaille bien ton calcul et justifie bien ce que tu fais (avec des phrases !)

On sait que ♦Ec=Ecf-Eci=W(P)+W(P)+W(R)=-mgh+F*d*cos@.
La variation de l'energie mécanique s'écrit aussi par: ♦Em=♦Ec+♦Ep
En remplaçant ♦Ec et ♦Ep par leur expression , on a donc:
♦Em=-mgh+F*d*cos@+mgh-0
=F*d*cos@
Ainsi, F=♦Em/d*cos@=7,88×10^5 N.
On sait que ?Ec=Ecf-Eci=W(P)+W(P)+W(R)=-mgh+F*d*cos@.
La variation de l'energie mécanique s'écrit aussi par: ?Em=?Ec+?Ep
En remplaçant ?Ec et ?Ep par leur expression , on a donc:
?Em=-mgh+F*d*cos@+mgh-0
=F*d*cos@
Ainsi, F=?Em/d*cos@=7,88×10^5 N.
Revois les relations pour le travail du poids, ton produit scalaire n'est pas bon ... Le schéma est utile à cette fin
Oui mais tu ne connais pas h pour mémoire ...
Ce que je vais te proposer est peut-être ce que tu as trouvé mais tu ne l'as pas expliqué / justifié dans ce que tu as écrit :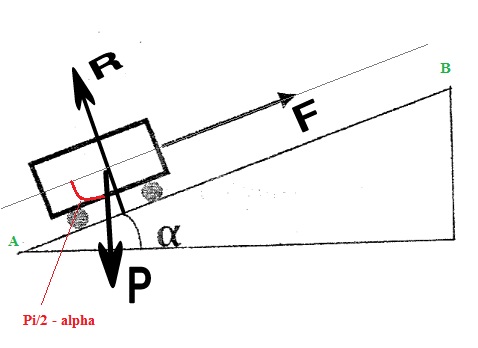


 .
.
 Okay merci!
Okay merci!
