Inscription / Connexion Nouveau Sujet
Energie mécanique
Bonjour,
J'ai des difficultés a répondre a la première question d'un exercice. Pouvez-vous m'aider à y répondre. Merci...
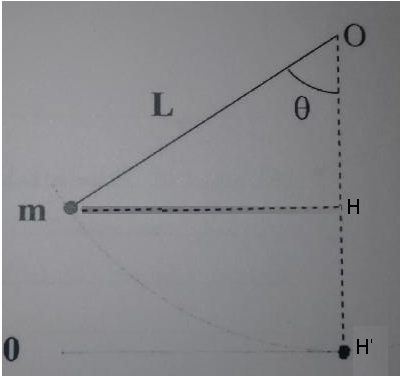
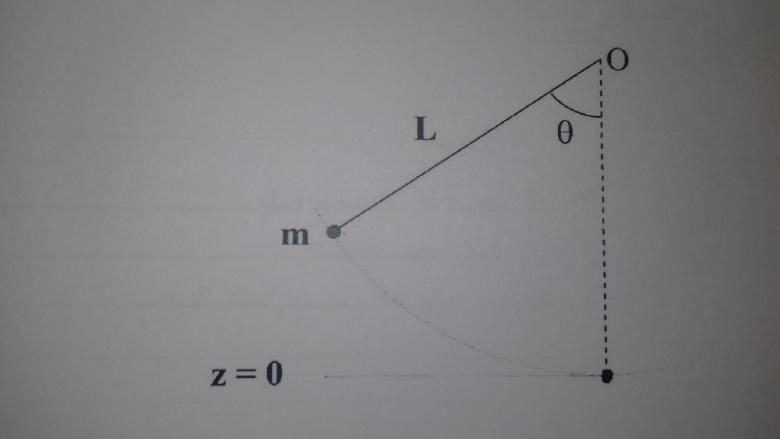
On considère un pendule simple constitué d'une masse ponctuelle m attachée à l'extrémité d'un fil inextensible de longueur L et de masse négligeable. La pendule est attaché à une de ses extrémités en O puis est écarté par rapport à la verticale d'un angle  = 60°
= 60°
On lâche alors la masse m sans vitesse initiale. On considérera que l'énergie potentielle de pesanteur est nulle lorsque la pendule se trouve à la verticale. Les frottements seront négligés.
1. Etablissez la formule littérale donnant l'énergie potentielle de pesanteur de la masse m dans sa position initiale en fonction de m,L,g et 
2. Comment varie l'énergie mécanique au cours de la descente de la masse. Justifiez
3. Déduisez-en l'expression de la vitesse de la masse à la verticale du point O.
4. Calculez cette vitesse dans le cas ou L=10m. On donnera le résultat en m.s^-1 et km.h^-1
Données
•g=9,81 m.s^-2
Je l'ai précisé :
HH' = OH' - OH
mais je vais détailler davantage :
OH' = L ( Longueur du fil )
OH = L * cos( ) calculé dans le triangle rectangle OmH
) calculé dans le triangle rectangle OmH
OH' - OH = L - L * cos( )
)
Super, c'est plus clair !!!
Voici ce que j'ai fait pour le reste:
2. Au cours de la descente de la masse, l'énergie mécanique diminue car l'altitude décroît et son énergie potentielle de pesanteur diminue. L'énergie cinétique augmente.
Pour la 3 je bloque...
Au cours de la descente de la masse, l'énergie mécanique diminue car ...... etc
Non.
Connais tu la définition de l'énergie mécanique ?
Connais tu sa principale propriété quand les frottements sont négligés ?
Si la réponse est "oui" , il faut appliquer cette définition et cette propriété.
Si la réponse est "non" à l'une ou l'autre de ces deux questions, il est inutile d'essayer d'aller plus loin dans cet exercice. Il faut d'abord apprendre le cours.
OK pour la définition.
Reste la propriété de cette énergie quand les frottements peuvent être négligés (C'est le cas ici)
C'est bien ça !
Tu peux donc maintenant corriger ta réponse :
Au cours de la descente de la masse, l'énergie mécanique reste constante.
Ce qui est perdu en énergie potentielle est compensé par un gain d'énergie cinétique.
Autrement dit : Connaître la valeur de l'énergie mécanique à un instant quelconque revient à connaître cette énergie mécanique à n'importe quel autre moment.
Exact ! il y a conversion de l'énergie potentielle de pesanteur en énergie cinétique.
3. Déduisez-en l'expression de la vitesse de la masse à la verticale du point O.
Comment puis-je répondre à cette question ?
Tu exprimes en fonction de m,g,L et  l'énergie mécanique au moment précis où tu lâches la masse.
l'énergie mécanique au moment précis où tu lâches la masse.
A ce moment là l'énergie mécanique est seulement de l'énergie potentielle.
Du coup, tu as aussi l'énergie mécanique de la masse au moment où elle passe à la verticale du point O.
Tu exprimes en fonction de m et v cette énergie mécanique.
A ce moment là l'énergie mécanique est seulement de l'énergie cinétique.
Il est alors tout simple d'obtenir l'expression de la vitesse de de cette masse.
Attention. Ce n'est pas une application numérique qui est attendue ici, mais une expression littérale de la vitesse en fonction de g, L et  ( la masse " m " disparait au cours du calcul )
( la masse " m " disparait au cours du calcul )
Et bien ce n'est pas mal du tout, à l'exception du signe " - " dont je ne vois pas l'origine :
Au départ :
Ec1 = 0
Epp1 = m*g*L*( 1 -cos ( ))
))
Em1 = 0 + m*g*L*( 1 -cos ( ))
))
A l'arrivée :
Ec2 = (1/2)*m*v²
Epp2 = 0
Em2 = (1/2)*m*v² + 0
Conservation de l'énergie mécanique :
Em2 = Em1
(1/2)*m*v² = m*g*L*( 1 -cos ( ))
))
Simplification par " m "
(1/2)v² = g*L*( 1 -cos ( ))
))
Il n'y a plus qu'à tirer " v " de cette expression.
Il est écrit dans mon cours que les mouvements sans frottements indique que la variation de l'énergie mécanique est nulle, soit:
 Em=
Em= Ec+
Ec+ Epp=0
Epp=0
D'où:  Ec=-
Ec=- Epp
Epp
Voilà d'où viens le signe "-"
Ce qui est écrit dans ton cours est exact, mais l'interprétation que tu en fais est erronée parce que tu confonds Ec avec ΔEc ainsi que Epp avec ΔEpp
ΔEc est la variation d'énergie cinétique c'est-à-dire la différence entre sa valeur finale (1/2)mv² et sa valeur initiale égale à 0
ΔEc = (1/2)mv² - 0 =(1/2)mv²
De même ΔEpp est la variation d'énergie potentielle c'est-à-dire la différence entre sa valeur finale égale à 0 et sa valeur initiale mgL(1-cos(θ ))
ΔEpp = 0 - (mgL(1-cos(θ )) = -mgL(1-cos(θ ))
Or d'après ton cours :
ΔEc = - ΔEpp donc
(1/2)mv² = - (-mgL(1-cos(θ ))
Soit finalement (1/2)mv² = mgL(1-cos(θ ))
qui est la même relation que celle que j'ai obtenue en raisonnant directement sur les énergies cinétiques et potentielles plutôt que de raisonner sur les variations d'énergies cinétiques et potentielles.
Okay c'est plus clair.
Voila pour la 3:
4. Pour la 4, g me bloque avec son unité m.s^-2. On me demande le resultat en m.s^-1. Quelle est la différence ?
Voila pour la 3:
C'est exact, mais ce sera plus lisible sous la forme :
Pour la 4, g me bloque avec son unité m.s^-2. On me demande le resultat en m.s^-1. Quelle est la différence ?
Pas d'inquiétude ! Le produit de l'accélération " g " par la longueur " L " a la dimension du carré d'une vitesse. Donc la racine carrée de ce produit g*L est bien une vitesse.
Oui, c'est exact.
Remarques :
a) v = 35,7 km/h est plus approprié que 35,66 km/h au vu de la précision des données de l'énoncé.
b) Il s'agit là d'une vitesse théorique, car les frottements (négligés ici) feront qu'une partie de l'énergie mécanique sera transformée en chaleur au cours de la descente.
La vitesse réelle sera toujours inférieure à cette vitesse théorique.