Inscription / Connexion Nouveau Sujet
energie cinetique
Bonsoir, salut à tous
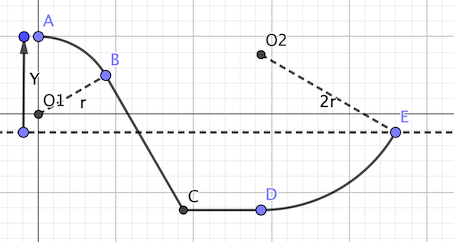
un chariot de masse m =200g de dimension négligeable est mobile sans frottement sur une piste dans plan verticale. La piste est formé des plusieurs parties ( voir figure 1)
1,a) le chariot abondonne sans vitess en A, déterminer ses vitesses en B , C, D E en fonction r g θ
b) Montrer que θ =π⁄3 sachant que la piste DE répresente un sixiéme de circonference de rayon r=1m
c) calculer numirequement VB,VD VC et VE
2)Soit Y la dénivellation entre A et E. en utilisant le théoreme de l'énergie cinetique, montrer que
Y=r(cosθ +2sinθ -1)
Reponses
1,a) Vb=  2gr(1-cos
2gr(1-cos )
)
Vc=Vd= 2gr(3-cos
2gr(3-cos ) car CD est rectiligne
) car CD est rectiligne
VE= 2gr(1+cos
2gr(1+cos )
)
b) on'a DE=2 r/6=
r/6= r/3
r/3
et DE= r donc
r donc =
= /3
/3
c) VB= 10 m/s
10 m/s
VC=VD=5 2m/s
2m/s
VE= 30m/s
30m/s
j'ai essaié de chercher Y, j'ai fai
D'apres TEC
1/2(mVE^2)-1/2(mVA^2)=mgy
er j'ai trouvé que Y=r(1+cos )
)
mais l'enonce ne veut pas ça
Merci à votre aide
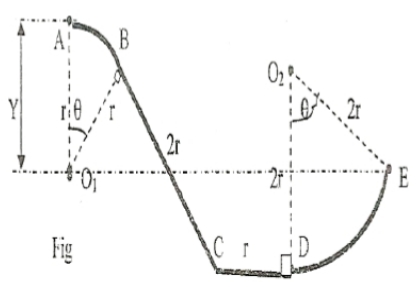
1a) B : OK. C : la longueur 2r est inclinée, donc la variation d'altitude n'est pas 2r.
1b) pas très clair : sur le dessin on voit un arc de cercle de rayon 2r, et dans le texte d'un rayon r.
2) pas très clair non plus : sur le dessin Y=r
Ce doit être le dessin qui est problématique : la longueur 2r (BC) a comme projection sur la verticale 2r également (O2D) ?!
Faut-il oublier le dessin ?
et pour la question 1)b)
L'arc DE=2r ou
ou  r
r
parce que l'exo nous dit que r mais dans le schema DE intercepte à un cercle de rayon 2r