Bonjour,

Question 1 :
Applique le théorème de l'énergie cinétique entre A et B, puis entre B et C

Bonsoir
Théorème de l énergie entre A et B
0,5 mVB au carré - 0,5 mvA au carre = W(p)+ W(R)+W(f)
O.5 mVB au carre = mgh + Wf)
Je suis bloqué s il vous plait comment trouver la hauteur et le travail du force de frottements
Entre B et C
0,5 mVc au carré - 0,5 mVB au carré=W(R)+W(p)+w(f)
0,5m(VB au carre-VC au carre =0+0-fxR
Vc =√-2f×R/m + VB au carré

Bonjour,

Avant de se lancer dans les calculs, il est indispensable de lire correctement l'énoncé.
Le texte de la question 1 donne tous les renseignements voulus pour calculer le travail des forces de frottements.

Pour la dénivellation entre A et B voir le schéma ci-dessous.

Donc
WP=mgh
h=r-cosa r
Wp=mgr(1-cosa)
Wf=-f×r
J attends votre reponse

Que dit l'énoncé au sujet des frottements à la question 1 ?

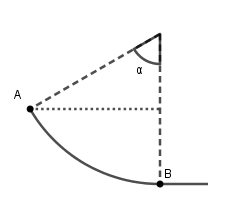
L énoncé  nous dire que la pisté ABC est verglacée. Les frottements sont alors suffisamment faibles pour négligés et ensuite que la résultante des forces de frottements constamment tangente a la trajectoire garde un module constant F sur tout le trajet ABC

En ce qui concerne la question 1 les frottements sont négligés.
Alors .... néglige les !

Le théorème entre A et B
0,5 mVB au carré -0.5 mvA au carre = mgr(1-cos a)
VB= √2gr(1-cos a)
Est ce que le résultat est
Correct?

Oui, ce résultat est correct.

Bonjour
1_2/ appliquons le théorème de l énergie entre B ET C
0,5 mvc au carre -mVB au carre=wp+wf+WR
Vc au carre = VB au carre
Voici ma réponse

J ai besoin d un exemple concernant
VC

Ok . comment trouver l expression de la vitesse VC

Rechercher toutes les forces qui s'exercent sur le skieur avec si possible leur direction, leur intensité.

Utiliser ensuite un des deux moyens suivants :
Appliquer le théorème de l'énergie cinétique ou bien
Appliquer la 2e loi de Newton.

Excuse moi. Sur le trajet  BC les forces de frottements existe
Donc on
0,5 mvc au carre-0,5 mVB au carré=wp +WR+wf
O,5m(vc au carré-VB au carré)=0+0-f×Bc.  Or Bc=R
Vc = √-2f×R/m + VB au carré
C est correct ?

Nous ne sommes pas d'accord.
Tu en es toujours à la question 1 . Je cite par un copier/coller ton énoncé.

"1/ lors d un premier essai la piste ABC est verglacée. Les  frottements sont alors suffisamment faibles pour être négligés.
Calculer dans ces conditions ,avec quelles vitesse VB et Vc  .le skieur passe en B et C"

Tu as trouvé l'expression de V_B (voir ton post du 25-12-18 à 22:35) mais tu n'as pas fait l'application numérique.
Tu n'as toujours pas établi correctement l'expression de V_C et bien sûr tu n'as pas fait l'application numérique.

En concernant VB
AN : VB =  √2×10×5(1-cos a)
Mais dans l énoncé on ne connait pas a

L'angle se calcule à partir du texte de l'énoncé :
Je cite :
"La partie AB représente un sixième de circonférence"

Je suis bloqué . s il vous plait aide moi a trouver la formuler pour que je puisse calculer l angle a

Il ne s'agit pas ici de "formule" mais de réflexion.

A quel angle correspond une circonférence entière ?
Donc à quel angle correspond un sixième de circonférence ?

Une circonférence entière correspondant  à 180°
Un sixième de circonférence =1/6 ×180
=180/6=30°
Donc a =30°

Ton raisonnement est bon, mais le point de départ est faux.
Une circonférence entière ne correspond pas à un angle de 180°

Je veux essayer encore mais si je ne trouver pas cette fois ci vous allez me donne la réponse correcte
Une circonférence entière correspondant à 360°
Un sixième de circonférence =1/6 ×360
=360/6
=60°

Cette fois ta réponse est exacte.
= 60° = /3 rad

VB=√2×10×5(1-cos60)
VB=√100×0,5
VB=√50
VB=7,07 m/s
Déterminer la vitesse vc
Système {skieur}
BF=le poids et la réaction normale
Appliquons TEC
0,5 mvc au carré-0,5 mVB au carré=Wp+WR
0,5 mVc au carré- 0,5 mVB au carre= 0+0
O,5 mVC au carré=0.5 mVB au carre
Vc=VB=7,07 m/s
Voici ma réponse concernant la question 1

C'est parfait !

1/1,exprimons Vc en fonction de m. R . f,g et VB
Système {skieur}
BF=le poids , la reaction normale et les forces de frottement
Appliquons TEC
0,5mVc au carré-0,5 mVB au carré=Wp+WR+Wf
0,5m(vc au carré-VB au carré)=0+0-fxBc or Bc=R
Vc=√-2f×R/m + VB au carre

Ton calcul est exact.
Mais ....
Je cite l'énoncé :
" 1/1_exprimer VC en fonction de m,R ,f et g "
alors que ton résultat est exprimé en fonction de m,R ,f et V_b

Autrement dit : Tu ne réponds pas à la question telle qu'elle est posée.

En fait dans la question 1/1 j ai oublié de mettre VB.donc excuse moi mais le résultat est correct

Donc, si je comprends bien :
Non seulement tu as oublié dans l'énoncé de la question 1/1 de mettre V_B mais tu y as mis "g" en trop.

Dans ce cas ton résultat



( dans lequel  figure "V_B" mais pas pas "g") est exact

Merci de vérifier la suite de ton énoncé.
S'il y a d'autres erreurs on y gagnera du temps.

J ai mal saisir la question voici la vrai question
On me demande d exprimer vc en fonction de m R ,f et VB

OK
Donc ton résultat est exact.

Ok
1/2 Exprimons VB en fonction de m R f et g
Système {skieur}
BF= le poids la réaction normale et les forces de frottements
Appliquons TEC
0,5 mvB au carré- 0,5 mvA = Wp +WR +Wf
0,5 mVB=Wp +Wf
Aide moi  a trouver Wp et Wf sur le trajet AB[bleu][/bleu]

Donc explique moi s il vous plait cette phrase pour que je puisse trouver une solution
La resultante des forces de frottement s constamment tangente a la trajectoire. Garde un module constant f sur tout le trajet ABC

Ce schéma devrait t'aider à exprimer les travaux des forces.
La force de frottement reste constamment tangente à l'arc AB au cours de son déplacement.
Sa norme f ne change pas.

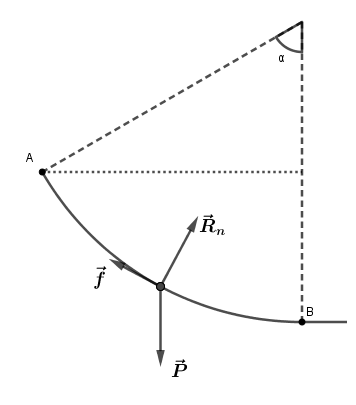
Voici ma réponse
Appliquons TEC
0,5 mVB au carre -0,5 mVA au carre = WP + WR + wf
0,5 mVB au carre =0+0-f×AB
Aide moi a trouver la distance AB

Je confirme que le théorème de l'énergie cinétique donne :



et puisque V_A=0



Je confirme aussi que le travail de est nul

En revanche le travail de   n'est pas nul !

La longueur de l'arc AB s'obtient facilement à partir des données de l'énoncé :
Je cite : "La partie AB représente un sixième de circonférence vertical de rayon R=5m "

On sait que
L arc AB=a/180 ×pi×R
L arc =60pi × 5/180
L arc AB=5pi/3
L arc AB=5,23  

Restons simples:
Périmètre : (2R) m
(1/6) de périmètre = (R/3) m

Eviter quand on peut les nombres décimaux.

Ok .ensuite on fait quoi

Ensuite ....
Tu exprimes le travail du poids entre A et B  et tu as alors tous les éléments pour exprimer V_B en fonction
de m, R, f et g ce qui est l'objet de cette 1\2

Appliquons TEC
0,5 mVB au carré=0+P×AB×cos(P,AB)-f ×AB
Comment trouver l angle (P,AB)et sur ce schéma je n arrive pas a trouver l expression de VB

Sur le trajet de l'arc AB l'angle entre la direction du poids et du déplacement change en permanence.
On ne peut donc pas calculer le travail du poids par la méthode que tu proposes.

Mais le travail du poids peut aussi se calculer par la relation :



relation dans laquelle " h " représente le dénivellement entre les points A et B
h peut être exprimé en fonction de R ( rayon de l'arc de cercle) et de

Remarque : L'énoncé impose la notation " R " pour le rayon de l'arc de cercle.
On ne peut pas utiliser la même notation pour la réaction de la piste sur le skieur.
C'est pourquoi pour moi cette réaction est notée

On z donc
W(p)=mgh
h=r-rcos a
W(p)=mgr(1-cos a)
Concernant les forces de frottement
La formule
Wf=-f×AB peut être utilisé aussi

OK pour le travail du poids :



L'énoncé (toujours lui !) précise que (je cite)
" la résultante des forces de frottements constamment tangente a la trajectoire"
ce qui revient à dire que l'angle entre la direction de la force de frottement et celle du déplacement ne change pas et reste égal à sur le trajet AB

On a bien :

Ok donc on
0,5 mVB au carré=mgr/2 -f×pi×R/3
0,5 m VB au carré=mgr(1-pi/3)-f×R×pi/3
0,5 mVB au carré=mgR-mgR×pi/3-f×R×pi/3
Simplification
0,5 mVB au carré=-f×R
VB =√-2f×R/m
Dans l expression il manque g je ne comprends pas aide moi a le retrouver

Ton calcul est faux dès la 2e ligne (de calculs)

Le rayon de l'arc de cercle est " R "
Que vient faire " r " dans ton calcul ?
Pourquoi le mgr/2 de la première ligne devient il  mgr(1-pi/3) à la ligne suivante ?