Inscription / Connexion Nouveau Sujet
Energie cinetique
Bonjour
J'ai besoin d'aide sur cet exo
Merci d'avance
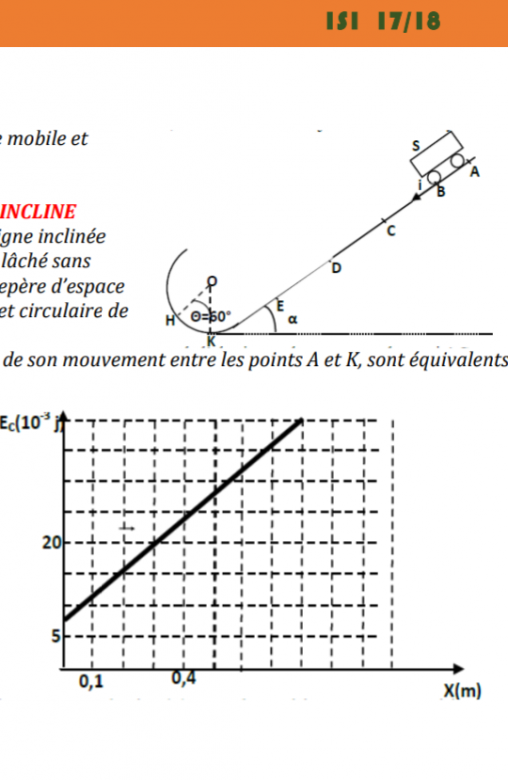
Un chariot (S) de masse m=50g se déplace sur une piste rectiligne inclinée d'un angle
=10° par rapport à l'horizontale. Le chariot est laché sans vitesse initiale du point A d'abcisse xa défini relativement au repère d'espace(B,
). Arrivé au point K avec une vitesse vk,le chariot suit un trajet circulaire de rayon r=0,1m et de centre O.
1.Les frottements auxquels sont soumis le chariot au cours de son mouvement sont équivalentes à une force f d'intensité supposée constante. A l'aide d'un dispositif appropprié ,on détermine la vitesse instantannée du chariot lors de son passage aux points B,C,D,E et K d'abcisses respectifs 0; 0,2;0,4;0,6;0,8. Ceci permet de tacer le diagramme ci -dessous correspondant à l'energie cinétique en fonction de l'abcisse x de son centre de gravité G.
a.En appliquant ce théorème au chariot entre la position B et une position quelconque d'abcisse x par rapport au repère(B,), montrer que Ec(x)=(mg.sin -f).x+Ec(B).
b. En exploitant le diagramme ,déterminer l'intensité de la force de frottement f et de l'abcisse de A xa.
c. Déterminer la valeur de la vitesse au point K.
2. On supposera tout type de frottement négligeable.
a.Représenter les forces qui s'exercent sur le chariot.
b. En appliquant le théorème ,montrer que vk2-vh2=2.g.r(1-cos
)
Pour la 1. j'ai fait
Ec(x)-Ec(B)=Wp+Wf(avec vecteurs sur les forces)
Ec(x)-Ec(B)=mgxsin-fx
Ec(x)=(mgsin-f)x +Ec(B)
C'est la 2.qui me pose problème
Salut,
F = mg.sin(alpha) - f (force résultante sur le chariot dans la direction et sens de l'ace des abscisses du repère)
Le travail de F sur une distance x est : W(x) = F*x = (mg.sin(alpha) - f).x
On a donc :
Ec(x) = Ec(au point B) + W(x)
Ec(x) = Ec(B) + (mg.sin(alpha) - f).x
Sur le diagramme (B à l(abscisse 0)), on lit Ec(B) = 7,7.10^-3 J (estimation)
Pour x = 0,8 (m), on liT Ec = 40.10^-3 J
--> 40.10^-3 = 7,7.10^-3 + (50.10^-3 * 9,81 * sin(10°) - f)*0,8
(50.10^-3 * 9,81 * sin(10°) - f) = (40.10^-3 - 7,7.10^-3)/0,8
0,0851744 - f = 0,040375
f = 0,0448 N (A arrondir ?)
-----
L'accélération du chariot est F/m = g.sin(alpha) - f/m = 0,8075 m/s²
Vitesse acquise sur une distance L = (AB)/2 :
AB/2 = a*t²/2
t² = AB/0,8075
v = a*t
v = 0,8075 * RCarrée(AB/0,8075) = 0,89861.RCarre(AB)
1/2.m.V² = 1/2.0,05.0,89861².(AB) = 0,0201875 AB
0,0201875 AB = 7,7.10^-3
AB = 0,38 m
--> L'abscisse de A est - 0,38.
---
Autrement : plus direct.
On prolonge la droite du diagramme de Ec = f(x) et on mesure l'abscisse où elle coupe l'axe des abscisses.
On trouve : x = -0,19
C'est l'abscisse de G avant le départ. Et comme G est supposé au milieu de la longueur AB --> AB = 2 * 0,19 = 0,38 m
--> L'abscisse de A est - 0,38.
-----
Ec au point K = 40.10^-3 J
1/2.m.VK² = 40.10^-3
1/2 * 0,05 * VK² = 40.10^-3
VK = 1,265 m/s (A arrondir) ?)
-----
2)
La différence d'altitude entre les points K et H est R*(1 - cos(theta))
Le travail du poids sur le trajet KH est donc : WP = - m.g.R*(1 - cos(theta))
On a donc 1/2.m.VK² - m.g.R*(1 - cos(theta)) = 1/2.m.VH²
...
Sauf distraction. 
Annuler
connectez vous