Bonjour,

Fais d'abord un dessin represantant le pendule
à sa position initiale c'est dire faisant avec la vecticale un angle ₀.
Represente ensuite le pendule dans une position intermédiaire faisant un angle avec la verticale.

Prend l'axe verticale Oz (O point d'attache du pendule) orienté vers le haut.

Appelle Z₀ l'altitude initiale de la bille et Z son altitude quand le pendule fait un angle

Tu sais que le travail du poids entre les 2 positions est mg(Z₀-Z)

Or tu dois savoir facilement calculer Z₀
et Z en fonction de la longueur du fil et des angles ₀ et

Oula c'est possible d'avoir un peu plus de détaille car moi et ce chapitre je comprends rien pour la Chimie pas de problème mais là......

Merci d'avance

Cherche un triangle rectangle pour utiliser les relations trigos

Skops

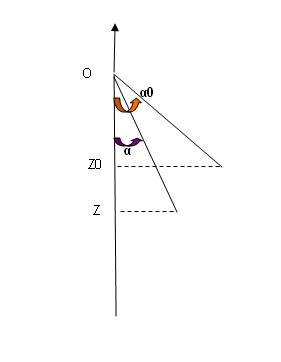
Voici un dessin pour mieux comprendre:

A la position initiale tu vois par exemple que la
bille est à l'altitude Z₀= -lcos(₀)

A une position intermédiaire faisant un angle avec la verticale la bille est à l'altitude Z= -lcos()

Le travail du poids entre la position initiale et la position courante du pendule est

Wp= mg(Z0-Z)= mgl (cos()-cos(₀))

Céest vrai que le dessin aide beaucoup merci ^^

b/ Calculer la valeur de la vitesse lorsque l'angle que fait le fil avec la verticale a pour valeur . calculer sa vitesse en B .

Comment peut on raisonner ? j'ai été abs pendant 5 jours dû à une grippe et je suis largué sur ce chapitre :/ . Comment peut on savoir le temps ? est-ce indispensable ?

b) Ecris la conservation de l'energie mécanique

A la position du lacher (angle initial ₀):

Em0= Ep0 + Ec0 = -mglcos(₀)

Car Ec0= 0 puisque le pendule est laché sans vitesse

A la position

Em= -mglcos() +1/2mv²

Em= Em0 d'où

v²= 2gl(cos()- cos(₀))

Application en B. Alors =0

V_B²= 2gl(1-cos(₀))

Merci encore ^^ c'est vraiment sympas . Je pense que c'est quand même un chapitre assez dificile non ?

Petite question bonus :p :
Le pendule oscille autour de sa position d'équilibre. Pour quelles valeurs de la vitesse de la bille est-elle nulle ?

A ton avis ?

Je propose alpha = ahpha0 et alpha = -alpha0

salut à vous tous,
pour faire les calcule on doit mettre que la boule n'a pas d'energie potentielle au point ou elle est en équilibre ?

Ah oui pour le b/ je tiens à m'excuser mais le fait d'utiliser l'energie mécanique c'est pas bon !!!! car nous avons pas vu l'energie mécanique . Desolé du retard

Bonjour,

Ecris simplement que le travail des forces de pesanteur est égal à l'énergie cinétique à tout instant après le lâcher.

De plus , je voulais ajouter à la question a/ il est impossible je crois de trouver alpha . La question à dû être mal formuler on peut que exprimer !

Oui, est une valeur quelconque 40°

Donc on exprime le travail et la vitesse en fonction de

Ok merci mais sinon pour le faite d'écrire juste que les forces de pesanteur = energie cinétique change la donne ? vu qu'il fait en fonction de l'energie mécanique ?

Non ça ne change rien. Car l'énergie potentielle de pesanteur résulte du travail des forces de pesanteur.

Bonjour!
J ai moi aussi cet exercice à résoudre... J ai réussi la question a) mais je ne comprend pas pour la b) comment Em= Em0
merci d avance

Bonjour, j'ai compris qu'il faut utiliser les règles de trigonométrie mais je ne comprends pas pourquoi il y a un moins devant:

"A la position initiale tu vois par exemple que la
bille est à l'altitude Z0= -lcos(0) "

Merci

Bonjour.

bsr merci j ai devoir demain et c est le meme exercice que je ne comprenais pas surtout la derniere questions ajouter par mon professeur:
reprendre toutes les questions  en prenant Z comme origine du repère.