Bonjour
Sans schéma fourni, je ne suis pas sûr d'avoir bien compris l'énoncé et surtout, impossible de connaître le signe du flux magnétique et le sens du courant induit. Que désigne l'angle ?

Salut

Salut, le schéma que l'exercice a proposé est

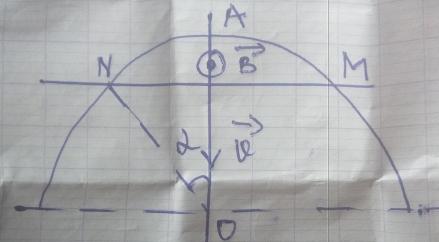
Tu n'as pas précisé sur ton schéma l'orientation du circuit induit que je suppose constitué de l'arc de cercle (MAN) et de la tige MN mobile à la vitesse v. Si tu veux écrire le flux magnétique sous la forme : , il faut orienter le circuit dans le sens inverse à celui de rotation des aiguilles d'une montre (sens trigonométrique), sinon, il faudrait poser :  .
Pour trouver S, tu peux procéder par différence :
1° : Exprimer l'aire S1 correspondant à la portion de disque délimitée par les rayons OM et ON. Sachant que l'aire du disque complet est a² et correspond à un angle de 2 rad, quelle est l'aire correspondant à 2 rad ?
2° : Exprimer l'aire S1 du triangle (OMN)
3° : Évidemment : S=S1 - S2
Je te laisse réfléchir...

Dans le triangle MNO :
S= r^2sina.cosa

Pour le demi cercle j'ai fait la règle de trois et j'ai trouvé :
S1= r^2.a
S=S1-S2, ça j'ai trouvé merci beaucoup.
cordialement

Flux=r^2.B(a-sina.cosa)
NB: a= angle alpha.
2) Par définition,
e=-d(flux)/dt, comment dérivé certe fonction trigonométrique?
cordialement

D'accord avec ce que tu as fait. Tu peux éventuellement simplifier un peu en passant à l'angle double ; en conservant les notations de l'énoncé :



Pour dériver, il faut utiliser la dérivée d'une fonction de fonction :avec les notations des cours de maths :



En posant :



Tu peux ensuite écrire que v est la vitesse du point H, milieu du segment MN :





Je te laisse dériver sur le modèle précédent et terminer... Pas facile au niveau terminale, cet exercice !

Hum je suis compliqué encore

Est-ce que je dois appliquer (u.v)'= u'.v+v'.u?
cordialement

Non ! Pour obtenir v à partir des indications que je t'ai fournies, tu dois juste exprimer la dérivée par rapport à t de a[1-cos()]. Je t'ai précédemment montré comment calculer la dérivée par rapport à t de sin() sachant que dépend de t... La méthode est analogue.

Je trouve que :
V=a'(1+a.sina)

Puisque tu n'utilises pas l'éditeur d'équations, je m'y perds un peu avec a le rayon et l'angle. Ici, le rayon a est fixe, on peut donc le sortir de la dérivation :



Comme l'angle dépend du temps, le raisonnement déjà fait conduit à :



Il ne te reste plus qu'à remplacer dans l'expression de , par cette valeur...

Je trouve que :
e=2BaVsinα
Pour la troisième question, j'ai appliqué la loi de Pouillet :
I= e/R= 2BaVsinα/R.
Mais la réponse dans le livre est:
I= BVsinα/R(α+sinα)
Cordialement

Mais d'après la figure, je trouve que :
r= AH/(1-cosα)
Comment trouver AH pour remplacer dans i ?
Cordialement

Bonjour Vanoise et Khalifa

@Vanoise :
Dans ton post du 26-08-19 à 15:01 ( et les suivants ) ta relation :


n'est pas homogène.
Je suppose que tu as oublié d'y entrer le champ magnétique.

@ Khalifa :
Attention !
R désigne la résistance du circuit par unité de longueur ( voir énoncé )

Odbugt1, J'ai remarqué ça, mais j'ai finalement compris et j'ai introduit B

Bonjour
Merci odbugt1 d'avoir relevé mon étourderie : je me suis concentré sur le calcul de S et de sa variation en oubliant le champ magnétique. Je récapitule les formules utiles après rectification :





Pour avoir la résistance électrique Re du circuit, il faut multiplier la résistance linéique par la longueur du circuit : la longueur de l'arc (MAN) et la longueur de la corde (MN).
Attention aux sens : avec le sens que j'ai défini au départ qui a conduit à poser , ce que tu as toi aussi posé,
on obtient e<0 et i<0 : le courant circule en sens inverse du sens positif choisi. Evidemment, si ton corrigé à choisi d'orienter le circuit en sens inverse, il a posé , ce qui conduit à e>0 et i>0.
Quelle que soit le sens d'orientation initialement choisi au départ de façon arbitraire, on obtient heureusement le même sens réel de courant. On peut d'ailleurs vérifier ce sens en utilisant la loi de Lenz mais je ne sais pas si cela est à ton programme.
En tout cas, il te faut bien revoir cette histoire de détermination du sens du courant induit...

On a juste énoncé la loi de Lenz et de Lenz-Faraday, mais on nous a pas montré comment trouver le sens du courant induit.

mais qu'est ce qu'une résistance linéique?

La résistance linéique est la résistance par unité de longueur (mesurée en /m) ; si tu préfères, la résistance du circuit est le produit de la résistance linéique (appelée ici très improprement R) par la longueur du circuit. Je t'ai expliqué comment calculer la longueur du circuit...
Mais le plus important dans tout cela est de bien comprendre les problèmes de signes. Souvent les étudiants ont des difficultés à ce sujet.
À toi de voir si cela t'intéresse car cela ne semble pas demandé ici : essaie de retrouver le sens réel du courant induit à partir de la loi de Lenz. Il faut reconnaître que cela est un peu subtil...

Tout reste à savoir, comment calculer la longueur de l'arc MAN. J'ignore vraiment les propriétés permettant d'obtenir ce resultat.

Par définition même de l'angle mesuré en radians, la longueur de l'arc est le produit du rayon par l'angle au sommet (voir ici par exemple : ). Ce qui donne ici :
longueur (MAN)=2a..
Pour la longueur de la corde MN, tu vas surement te débrouiller avec les triangles rectangles et la trigonométrie. On obtient le résultat de ton corrigé mais avec un signe négatif comme déjà expliqué compte tenu de l'orientation initiale différente du circuit.