Bonjour
Qu'as-tu réussi à faire pour l'instant ? Qu'est ce qui te bloque exactement ?

1.a Équation différentielle du mouvement
Bilan de forces :
- la force électrique ;
- la force de frottement ;
- le poids

Peut - on appliquer le Théorème du centre d'inertie comme en mécanique ?
J'avoue que je n'ai jamais corrigé un exercice de ce type.

Oui. On reste ici en mécanique classique. Comme toujours lorsqu'on étudie le déplacement de charges électriques, le poids est d'influence totalement négligeable devant les autres forces. Tu peux donc le négliger. Tu peux alors montrer que, compte tenu des conditions initiales, le mouvement d'un électron est rectiligne avec pour direction et sens ceux du vecteur (. Tu peux donc projeter la relation fondamentale de la dynamique sur un axe astucieusement choisi. Ici : q=-e.

Comme tu fais pour comprendre que le sens du mouvement est celui de ?

Il n'y a pas de vitesse initiale et la seule force motrice est la force électrique .

PS : montrer que le mouvement est rectiligne est moins évident qu'il n'y paraît. La démonstration présente des points communs avec celle qui permet de montrer qu"un pendule simple, écarté de sa position  d'équilibre et abandonné sans vitesse initiale, oscille dans le plan vertical fixe contenant la position initiale et le point fixe d'accrochage du fil. (le repère terrestre est supposé galiléen bien sûr).

J'ai bien compris !
Maintenant le TCI :
Suivant le sens positif du mouvement :

F - f = m.a

Donc

D'où l'équation différentielle :

D'accord. Maintenant, tu admets que la solution générale est la somme de deux solutions :
* la solution particulière Vp correspondant au cas particulier V'=0 à chaque instant ;
* la solution Vh de l'équation homogène c'est à dire de l'équation différentielle avec constante nulle :


Tu as rencontré ce genre d'équation différentielle homogène  dans d'autres domaines de la physique-chimie...

• la solution particulière est :

• la solution particulière est : aidez-moi moi ici svp

Au niveau terminale, tu peux te contenter de vérifier qu'une expression de la forme :



est bien solution de :

Cela te permet d'exprimer en fonction de k et m. Pour la constante A, il suffit de considérer que la solution générale :



vérifie : V_(t=0) = 0.

D'accord, mais la question 1.b) demander de passer par les intégrales pour exprimer V = f(t)

Intégrer une équation différentielle signifie simplement en trouver la solution. La théorie mathématique est traitée au niveau bac+1. Au niveau terminale, tu peux te contenter de vérifier que Vh est solution de l'équation différentielle homogène pour une valeur à préciser de puis que V_(t) est bien solution de l'équation différentielle générale.

D'accord



est solution de :   signifie que



Donc

Alors

La solution générale est :




A t = 0, V(t=0) = 0, je tire A et je trouve A = -eE/m

Donc

Plus simplement :  

Après tout, tu peux tenter la résolution de la façon suivante. On part de l'équation différentielle homogène que l'on écrit sous la forme :



puis on divise les deux terme par Vh.



C'est à ce niveau que l'on “intègre”, c'est à dire que l'on écrit qu'une primitive par rapport à t du terme de gauche est égal à une primitive par rapport à t du terme de droite, tout cela bien sûr, à une constante près.



Petite astuce : on écrit la constante sous la forme ln(A) où A est une constante positive.




Tu devrais pouvoir terminer...

Nous avons posté à peu près au même instant.
D'accord et j'ai bien compris.
Maintenant la question 1.c) sur le calcul de la vitesse limite :

Lorsque t + ; V tend vers une limite V_L qui vaut :

  

C'est bien cela. L'exponentielle tend vers zéro, ce qui conduit à ton résultat !

D'accord.

  ;  donc

AN :  

Je trouve un résultat que je n'ose pas écrire écrire ici

Je crois qu'il y'a une erreur de données.

Je crois surtout qu'il y a une étourderie que j'aurais d'ailleurs dû repérer plus tôt...
L'équation différentielle obtenue précédemment est correcte :

La solution particulière correspond à :


D'ailleurs l'énoncé fournit la valeur de V_p=V_L et demande d'en déduire la valeur de k.
Remarque : note bien la valeur numérique très faible de cette vitesse. Contrairement à une idée reçue, les électrons de conduction se déplacent très lentement dans un conducteur mais, comme ils sont très nombreux et transportent une charge électrique très importante (environ 96500 coulombs par mole d'électrons), il est possible d'obtenir des intensités importantes.

Oh je vois !

La solution générale est :




A t = 0, V(t=0) = 0, je tire A et je trouve A = -eE/k

Donc

Plus simplement :  

Ainsi lorsque t + ; V tend vers une limite V_L qui vaut :

  

Soit

Si je comprend bien, on ne demande pas de calculer ici la valeur numérique de V_L, n'est-ce pas ?

Oui, c'est ce que j'ai compris de l'énoncé de la question 1d)
Pour 1e) tu as intérêt à poser :
: constante de temps de façon à faire intervenir une exponentielle de la forme : .

Question 1.d)

De la relation de V_L, on trouve :



k = 3,6.10^-25 J.s

D'où vient cette unité pour k ?

Oh j'ai commis une erreur sur l'unité.
Au numérateur, le produit eU est en joule.
Au dénominateur, V_L.l en m².s^-1

Donc k = 3,6.10^-25 J.m^-2.s

Raisonnement correct. On peut trouver un peu plus simple à partir de f=k.v ; cela conduit à k mesuré en kg/s.

OK.
Je préfère alors k = 3,6.10^-25 N.s.m

Calcul de la mobilité



= 4,4.10^-3 m²/V.s

Tu es sûr de la puissance de 10 pour la valeur de k ?
A propos de l'unité de k : sachant qu'une force est homogène au produit d'une masse par une accélération, on peut utiliser le N.s/m mais le kg/s est quand même plus simple !

OK

k = 3,6.10^-17 kg/s

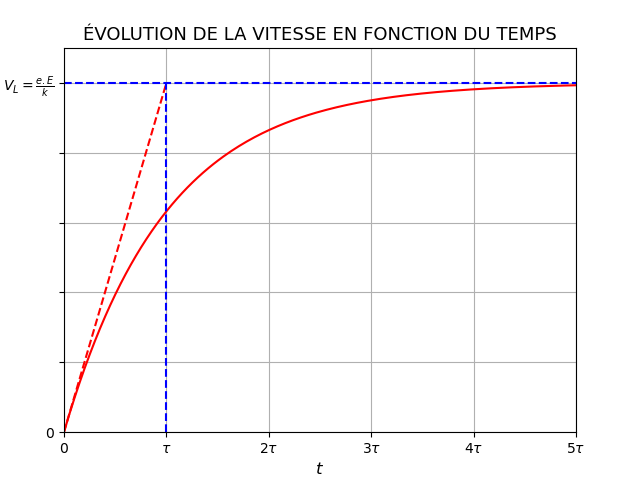
Maintenant la question 1.e) consiste à tracer V=f(t) qui est une fonction exponentielle décroissante.

OK pour k.

Quelle étourderie de ma part !
Oui, V(t) est une fonction exponentielle CROISSANTE, quelque soit t [0 ; +[

L'équation V = V_L est l'asymptote horizontale.

La courbe commence à l'origine du repère et tend vers vers la branche asymptotique V_L.

C'est ça ?

Oui ! Ton équation peut s'écrire :


En plus de ce que tu as écrit, on peut dire :
L'asymptote est quasiment atteinte au bout d'une durée de l'ordre de 5. Cela s'explique par le fait que, pour t>5, exp(-t/)<e^-5 soit

exp(-t/)<3,7.10^-3 soit exp(-t/) 0
C'est pour cette raison que l'on considère souvent que la durée du régime transitoire est d'environ 5.
A noter éventuellement, pour le tracé de la courbe : la tangente à la courbe en t=0 coupe l'asymptote horizontale en t=.

Merci.
2) Expression de l'intensité I du courant :

I.t a la dimension physique d'une charge électrique alors que n.e à la dimension d'une charge divisée par un volume. Ta formule est donc fausse car non homogène.
La constante de temps étant extrêmement petite, on peut considérer que le régime permanent est atteint à chaque instant. Pendant une durée t, chaque électron parcourt la distance V_L.t . Imagine une section droite du conducteur d'aire S=a.b ; les électrons qui vont traverser cette section droite entre les instants de dates zéro et t sont les électrons situés à la date zéro, avant la section droite, à une distance de celle-ci inférieure à V_L.t.
Bref : la charge I.t représente la charge mobile contenu à la date zéro dans le parallélépipède rectangle de longueur V_Lt et de section droite d'aire S=a.b, donc dans le volume de conducteur : a.b.V_L.t
Je te laisse continuer...

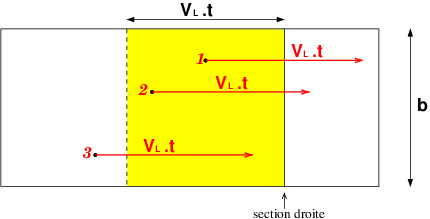
Petit schéma pour illustrer mon précédent message. J'ai représenté une vue de dessus du ruban avec les positions (numérotées de 1 à 3) de trois électrons à la date zéro. Entre l'instant de date zéro et celui de date t, chaque électron parcourt la distance V_L.t. On voit bien que seuls les électrons 1 et 2 traversent la section droite de référence pendant la durée t.