Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

électricité association de résistances

Posté par simon65 (invité) 18-08-05 à 18:41

bonjour,
voilà un schéma électrique qui m'a paru simple au départ mais aprés réflexion je pars un peu dans tous les sens. Pourriez-vous m'aider. Merci d'avance

Calculer la résistance équivalente RAB . Données : Ri = i ohm ; R = 0,5 ohm.




électricité association de résistances

Posté par
charlynoodlesre : électricité association de résistances 18-08-05 à 19:18

Bonjour

Mes cours d'électricité datent un peu mais je pense qu'il faut :


A gauche : R1 et R2 sont en parallèle, tu peux alors calculer la résistance équivalente :


\frac{1}{REQ}=\frac{1}{R1}+\frac{1}{R2}

\frac{1}{REQ}=\frac{R2}{R1*R2}+\frac{R1}{R1*R2}

\frac{1}{REQ}=\frac{R1+R2}{R1*R2}

REQ=\frac{R1*R2}{R1+R2}

Il en est de meme pour la partie parallèle gauche du circuit

Finalement on a trois résistances en série : REQ R REQ

Donc la résistance équivalente vaut

Réquivalentefinale = 2REQ+R=REQ=\frac{R1*R2}{R1+R2}+R

Voili voilà

Charly

En espérant que ça soit juste,je vais avec mes souvenirs

Posté par
charlynoodlesre : électricité association de résistances 18-08-05 à 19:21

Oups c'est

Réquivalente finale = \frac{2*R1*R2}{R1+R2}+R

R1=1 ohm
R2=2 ohm

donc

Réquivalente finale =\frac{2*R1*R2}{R1+R2}+R=\frac{2*1*2}{1+2}+0.5=\frac{4}{3}+\frac{1}{2} =\frac{11}{6} ohm

Voilà

Posté par simon65 (invité)re 18-08-05 à 20:02

Merci beaucoup Charlynoodles. J'avais fait comme toi mais je viens de trouver sur le net que la réponse serait:

Réq= ( 2R1*R2 + R ( R1+R2)) / ( R1+R2+2R)

Mais il n'y a pas de détails sur ce résultat. Quelqu'un saurait-il comment faire?
Merci d'avance

Posté par
J-Pre : électricité association de résistances 18-08-05 à 20:37

Attention Charlynoodle, R1 et R2 ne sont pas en // (elles le seraient si R valait 0)

On n'a pas non plus les 3 parties que tu mentionnes en série.

Et malgré tout cela la réponse finale semble correcte ...

hasard ?
-----------------------------------


Une façon parmi d'autres de faire:

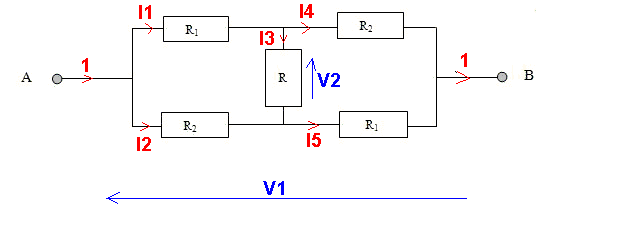
On fait comme si on injectait un courant de 1 A comme montré.
-----

On écrit les équations des mailles et des noeuds.

I1 + I2 = 1
I3 + I4 = I1
I2 + I3 = I5
V2 + R1.I1 - R2.I2 = 0
V2 - R2.I4 + R1.I5 = 0
V1 = R2.I2 + R1.I5
V2 = R.I3

Si tu veux trouver une solution littérale, il faut résoudre ce système en gardant les lettres.

On doit garder V1 et éliminer I1 à I2 ainsi que V2)
On aura donc V1 = f(R1, R2, R)

R(AB) = V1*1 (puisque on a injecté 1 A)

Et donc on a alors R(AB) = ...
-----
Avec les valeurs numériques de l'énoncé:

I1 + I2 = 1
I3 + I4 = I1
I2 + I3 = I5
V2 + I1 - 2.I2 = 0
V2 - 2.I4 + I5 = 0
V1 = 2.I2 + I5
V2 = 0,5.I3

Le système résolu donne V1 = 11/6   (à vérifier)

R(AB) = V1*1 (puisque on a injecté 1 A)
R(AB) = 11/6 Ohm

(Je retombe sur la valeur de Charly mais c'est un hasard probablement)

Il y a bien d'autres manières d'y arriver.
-----
Sauf distraction.


électricité association de résistances

Posté par
J-Pre : électricité association de résistances 18-08-05 à 21:51

Il y a une bisbrouille quelque part, je recommence.

Avec le même dessin:

On peut se passer de V1 et V2

On a le système:

I1 + I2 = 1
I3 + I4 = I1
I2 + I3 = I5
1.I1 + 0,5.I3 = 2.I2
1.I5 + 0,5.I3 = 2.I4

Résolu, on a:
I1 = 0,625
I2 = 0,375
I3 = 0,25
I4 = 0,375
I5 = 0,625

V1 = 2.I2 + I5  = 1,375

Et donc R(AB) = 1,375 Ohm
-----
Sauf nouvelle distraction.  

Posté par
charlynoodlesre : électricité association de résistances 18-08-05 à 21:58

Rien à dire J-P : moi et l'électricité ça fait deux !!

Heureusement que t'es là : j'ai meme pas pensé aux lois des noeuds et des mailles !

Chapeau . J'ai bien fait de laisser tomber la physique lol !!

Charly

Posté par jmix90 (invité)re : électricité association de résistances 18-08-05 à 23:34

Bonjour,


Pourquoi a t'on ca svp:

---------------------------------------------------------
1.I1 + 0,5.I3 = 2.I2
1.I5 + 0,5.I3 = 2.I4
---------------------------------------------------------

Merci

Posté par
J-Pre : électricité association de résistances 19-08-05 à 08:41

1.I1 + 0,5.I3 = 2.I2

loi des maille dans la maille constituée par R, et les R1 et R2 de gauche sur le dessin.

On a, la somme des tensions dans la maille étant nulle:

R.I3 + R1.I1 - R2.I2 = 0
0,5.I3 + 1.I1 - 2.I2 = 0
1.I1 + 0,5.I3 = 2.I2
-----
1.I5 + 0,5.I3 = 2.I4

Pareil que ci-dessus mais pour la maille de droite constituée de R et des R1 et R2 de droite sur le dessin.
-----
Remarque:
Si on repart du système donné dans ma première réponse, on trouve aussi R(ab) = 1,375 Ohm.
J'avais du faire une erreur de calcul quelque part.
-----
Sauf distraction.  

Posté par jmix90 (invité)re : électricité association de résistances 19-08-05 à 12:46

Ho aurant pour moi, j'avais pas vu les valeurs des Résistances


Amicalement,

Posté par simon65 (invité)re association de résistances 19-08-05 à 14:59

Merci beaucoup à JP et aux autres pour toutes vos explications!
Encore merci. Au fait, j'ai demandé à mon cousin une solution à cet exo et il m'a expliqué le théorème de Kennely qui s'avère très intéressant dans ces cas-là.
voilà merci à tous

*** message déplacé ***

Posté par
Océanere : électricité association de résistances 19-08-05 à 15:00

Pourquoi ne pas poster tes remerciements à la suite de ton topic ?

Posté par simon65 (invité)re 19-08-05 à 15:05

je suis désolé je suis novice sur le forum et je me suis trompé.
Encore désolé

Posté par
Océanere : électricité association de résistances 19-08-05 à 15:34

Ce n'est pas grave, tu le sauras pour la prochaine fois comme ça
Et c'est très gentil de ta part de penser à remercier les personnes qui t'ont aidé, c'est le principal

Posté par
soucoure : électricité association de résistances 23-08-05 à 17:57

Bonjour,

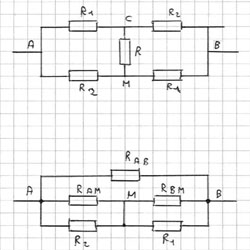
N'y aurait-il pas une solution trivial utilisant le théorème/transformation de Kennely ?

Avec \displaystyle R_{AB}=\frac{\:\frac{1}{R_0}+\frac{1}{R_1}+\frac{1}{R_2}\:}{\frac{1}{R_1}\frac{1}{R_2}}=\frac{R}{RR_1+RR_2+R_1R_2}, R_{AM}=\frac{R_1}{RR_1+RR_2+R_1R_2} et R_{BM}=\frac{R_2}{RR_1+RR_2+R_1R_2}

Ce qui donne R_{eq}=\frac{R_{AB}\(\frac{R_{AM}R_2}{R_{AM}+R_2}+\frac{R_{BM}R_1}{R_{BM}+R_2}\)}{R_{AB}+\frac{R_{AM}R_2}{R_{AM}+R_2}+\frac{R_{BM}R_1}{R_{BM}+R_2}}

Reste plus qu'à simplifier...

Qu'en pensez vous ?

Merci

électricité association de résistances

Posté par
soucoure : électricité association de résistances 23-08-05 à 18:04

Mince, il y a un incohérence

- Lire Kennelly

- R_{AB}=\frac{\:\frac{1}{R_0}+\frac{1}{R_1}+\frac{1}{R_2}\:}{\frac{1}{R_1}\frac{1}{R_2}}=\frac{RR_1+RR_2+R_1R_2}{R} ainsi de suite...

Désolé et merci

Posté par
soucoure : électricité association de résistances 23-08-05 à 18:05

Aie, R_{AB}=\frac{\:\frac{1}{R_0}+\frac{1}{R_1}+\frac{1}{R_2}\:}{\frac{1}{R_1}\frac{1}{R_2}}=\frac{RR_1+RR_2+R_1R_2}{R}

Posté par simon65 (invité)re 24-08-05 à 17:13

Mais cela doit-être possible de le résoudre avec les résistances en série et en parallèle non?

Posté par
J-Pre : électricité association de résistances 24-08-05 à 17:59

C'est loin d'être toujours possible.

Su tu veux essayer par exemple avec le circuit décrit ci-dessous.

Tu places une résistance de 1 Ohm sur chacune des arètes d'un cube et tu cherches la résistance équivalente entre les sommets les plus éloignés du cube.

Donc si tu as le cube ABCDEFGH, tu cherches la résistance entre A et G.


Si tu y arrives avec des associations série et parallèle ...
il y a toutes les chances que tu te sois planté.



Posté par
soucoure : électricité association de résistances 24-08-05 à 19:12

J-P, ton dernier message s'adresse t-il à moi ou à simon65 ?

Remarque: dans mon calcul, j'avais écrit R_{AB}=\ldots, je pense que vous aviez compris que cela ne représente le nom donner à une résistance particulière et non pas la résistance équivalente de l'ensemble.

Posté par
J-Pre : électricité association de résistances 24-08-05 à 19:39

soucou

Le message était pour simon65, mais est valable pour tous.

Il n'est pas toujours possible de n'utiliser que des mises en // ou en série de résistances pour se tirer d'affaire.

Il existe bien évidemment d'autres méthodes que celle que j'ai données ici.

Je n'ai pas vraiment regardé la solution que tu proposes mais elle me fait mal aux yeux.

Les formules que tu donnes pour RAM er RBM ne donnent pas des Ohms mais bien des Ohm^-1, je suppose qu'il faut inverser ce que tu as donné comme formules.

Dans ces conditions, je trouverais:
RAB = 7
RBM = 1,75
RAM = 3,5

Ce qui donne Req = 1,5 Ohm et cela c'est faux.

Il y a une bisbrouille quelque part, mais je n'ai pas cherché où.
-----

Posté par
soucouYoupi 24-08-05 à 20:53

Oui J-P, il y a une bisbrouille, et pas qu'une d'ailleurs.

D'une part, du faite qu'il faut inverser le numérateur et le dénominateur dans la transformation de Kennelly. Mais bon je l'avais signaler avec les deux messages suivant, ou du moins j'avais éssayé.

De même le théorème de Kennelly aurait plutôt stipuler R_{AM}=\frac{RR_1+RR_2+R_1R_2}{R_2}=3.5, le dénominateur n'est pas R_1 bel est bien R_2, idem pour R_{BM}, changer R_2 par R_1.

Je trouve au final, la même valeur que la votre...



Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 237 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !