Inscription / Connexion Nouveau Sujet
écart angulaire - diffraction des ondes sonores.
Bonjour,
Je suis face à un problème que je n'arrive pas a résoudre. Je suis en DAEU B par correspondance et je n'ai pas de prof disponible pour m'aider.
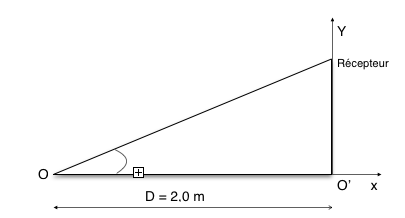
La figure1 (le triangle) est le schéma d'une diffraction d'onde sonore ou O est une fente à travers laquelle l'onde sonore passe. Elle se diffracte et est mesuré par le récepteur.
voici les question qui sont posé:
1) On déplace le récepteur selon l'axe Oy, et on relève l'amplitude de l'onde en fonction de l'angle θ.
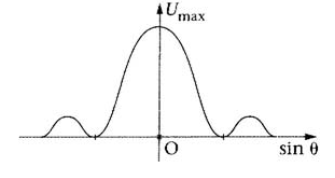
On trace ensuite la courbe Umax = f(sin θ). Quel phénomène cette courbe met elle en évidence?
Là on est sur la figure2, le graphe avec Umax pour l'axe y et Sin θ pour les abscisse. (θ est l'angle Ô).
Bon la je dirait que c'est un phénomène d'interférence mais déjà je suis pas sûr...
Ensuite:
2) Déterminer la largeur d de la fente (donc chez nous O)sachant que, lorsque θ = 18°, l'amplitude du signal est minimum. On montre que les abscisses des deux minima sont:
x1 = +λ/d et x2 = -λ/d
Et alors la je suis perdu. je sais que je doit utiliser de la trigonométrie mais je ne sais pas par quoi commencer, sans compté que je ne voit pas du tout comment utiliser le graphe.
Bref j'ai besoin d'aide!
Merci d'avance!
Quentin.
PS: 3 donnée que j'ai obtenue au début de l'exercice peuvent surement aider: λ=0,017 m, période =5.10-5 s et fréquence = 20 kHz
Hello Kuk
Bon la je dirait que c'est un phénomène d'interférence mais déjà je suis pas sûr...
La fente en O agit comme une source quasi ponctuelle, "quasi" car en fait chaque point de la fente devient une source ponctuelle et donc une onde émise de 2 points différents de la fente arriveront en un point de l'axe 0z avec un déphasage. Et alors selon la valeur du déphasage, les ondes issues des 2 points se cumulent ou s'annulent => figures d'interférence
2
On montre que les abscisses des deux minima sont:
x1 = +λ/d et x2 = -λ/d

notons ymin l'abcisse du premier minimum, en reprenant tes notations par ailleurs:
Le premier minimum est obtenu pour
Donc (en prenant le côté positif de l'axe)
Ce que tu connais, c'est
 correspondant à ce ymin
correspondant à ce ymin
La figure géométrique que tu as fourni te rappelle que
Donc
Est ce que cela t'éclaires ... sans trop d'interférences?
Le premier minimum est obtenu pour
ymin = +/- λD/d
Ce qui m'embrouille c'est le passage du graphique a la géométrie... Là par exemple comment il faut réfléchir pour "coupler" le D et λ/d?
Quand tu parle de ymin, tu place le point d'abscisse sur le triangle ou sur le graphique? ou les deux en même temps?
Pour la suite si tgθ signifie bien "tangente de θ" je comprend le raisonnement. Mais comment passe-t-on de +/- λ/d à λD/d, cela demeure une mystère dans ma tête...
Si-il te plais n'hésite pas a détailler, car cela fait env 10 ans que je n'avais pas fait de maths et de physique donc il y as des truc tout simple qui m'échappe..
De nouveau merci d'avance!
hum hum
Bon je vais essayer de résumer:
Tu as une onde sonore qui se déplace le long de l'axe Ox (en venant des x négatif)
En 0, elle est arrêtée (disons par un plan vertical) et ne peut plus progresser que via une fente horizontale orientée perpendiculairement au plan xOy (axe 0z donc)
Pour les raisons évoquées plus haut (diffraction par une fente) se forment des figures d'interférences.
En promenant un récepteur (un micro donc puisqu'il s'agit d'ondes sonores) le long de Oy, ce récepteur va enregistrer des maximum et des minimum d'intensité sonore. C'est le schéma Umax/sin que tu indiques.
que tu indiques.
Le lien entre  et y est le suivant:
et y est le suivant:
(relation trigonométrique que reflète ton 1er schéma)
La seule chose que tu dois admettre, c'est la relation
Il y a une initiative sympa par les élèves de Normale Sup sur le sujet: ![]()
Le passage du "graphique" à la "géométrie" est il moins embrouillé? Si non, n'hésite surtout pas (comprendre c'est aussi être capable d'expliquer!)
PS: tg(x) est une "ancienne" notation (à laquelle je suis resté fidèle) pour la fonction tangente d'un angle exprimé en radian (tan était alors réservée pour les angles en degré). Cette différentiation a aujourd'hui disparu



