Bonjour,
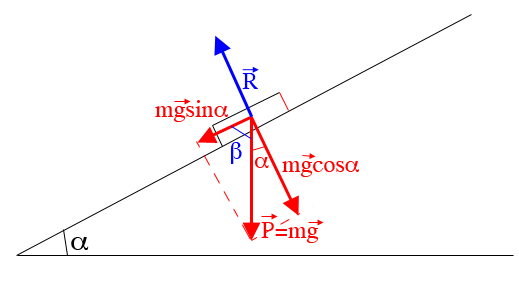
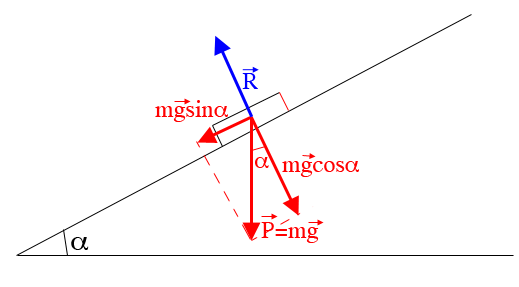
Le poids est vertical et se décompose en deux composantes.
L'une des composantes mgcos, verticale par rapport au plan incliné,est équilibrée par la réaction du support.
L'autre est parallèle au plan incliné et c'est mgsin.
Si ça ne te suffit pas, je ferai un schéma...
Pour retrouver l'angle , il faut utiliser les angles à côté perpendiculaires (qui sont égaux, comme chacun sait...).

Pouriez vous me faire un schéma svp ? car je confond surtout le mgcos et le mgsin . merci d'avance !

Ci-joint le schéma...
On retrouve l'angle du plan incliné (en rouge) parce qu'il s'agit d'angles à côtés perpendiculaires.
  est la réaction du support (perpendiculaire au plan incliné s'il n'y a pas de frottements).
C'est le b-a  ba de la mécanique du plan incliné.
Il faudra toujours appliquer ça pour un plan incliné

Merci beaucoup ! Cependant je ne comprend pas comment on peut différencier les deux composantes ici ?
Je veux dire es-ce qu'on peut par exemple inversser le mg sin et le mgcos ou bien c'est toujours le cos qui est vertical ?

Il faut évidemment tenir compte de certains rudiments mathématiques tels que par exemple :

- Des angles à coté directement perpendiculaires sont égaux.
- Et connaître aussi les relations liant les cos et sin des angles aux différents cotés dans un triangle rectangle.

C'est un minimum à savoir.

Il faut cesser de retenir des formules par coeur au lieu de comprendre ce qu'elles signifient vraiment

Comme l'a écrit J-P, il y a des choses qui sont des mathématiques de base qu'il faut savoir.
1) les angles à côtés perpendiculaires sont égaux... Je n'insiste pas.
2) On ne peut pas inverser m g cos et m g sin sachant où se trouve l'angle et connaissant les règles élémentaires de trigonométrie dans le triangle rectangle, à savoir :
cosinus = côté adjacent / hypoténuse
sinus = côté opposé / hypoténuse
tangente = côté opposé / côté adjacent

J'aurais tendance à dire que le cos est toujours vertical par rapport au plan incliné mais il faut se méfier. Je ne trouve pas d'exemple sur le moment qui dit le contraire. Mais il faut apprendre le minimum de choses par coeur. Il faut refaire la démarche à chaque fois. C'est le plus sûr moyen de ne pas se tromper.

J'ajoute afin que les choses soient bien claires (ou aussi claires que possible) que :
1) On a  
2)

dans le cas où il n'y a pas de frottement...

Ok merci , sinon pour le mgsin je ne vois pas ou se trouve le sur la figure !Pouvez vous me le montrer svp ? merci d'avance!

est sur le schéma que j'ai envoyé. A l'origine, est l'angle du plan incliné (en noir). Avec les angles à côtés perpendiculaires, on retrouve entre   et la perpendiculaire au plan incliné (en rouge).
On retrouve donc entre    et  

ce que je veut dire c'est l'autre angle   ce trouve t-il entre P et mgsin(pour le mgsin) ?

Bonjour Marc, si tu as le temps pourrais tu jeter un coup d'oeil à mon problème? https://www.ilephysique.net/sujet-equation-titrage-240787.html Merci beaucoup
Désolée du dérangement

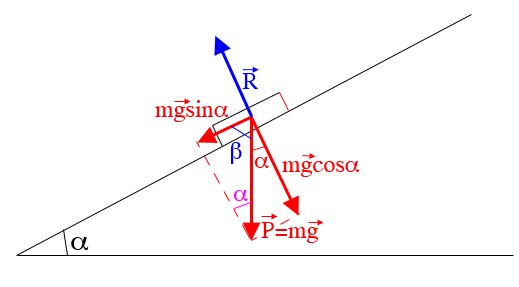
Sur le schéma joint, j'ai appelé l'angle entre et sa projection sur un axe parallèle au plan incliné (ce qui est appelé m g sin).
Dans une projection, c'est le cosinus de l'angle qui intervient. Donc la projection de   sur cet axe est donc m g cos.
Mais  
Autrement dit, et sont complémentaires.
Or :  
relation de trigonométrie bien connue (ou qui devrait l'être).
C'est ainsi que l'on obtient la projection de   sur cet axe .
J'espère avoir répondu à la question et avoir été clair.

J'ai oublié de joindre le schéma.

OK Romane

Si je comprend bien le côté adjacent est mg cos . Sinon pour le côté mg sines-ce que ça doit pas être le côté opposé(vu que sin= O/H) ?

Non parce que la projection du poids sur l'axe parallèle au plan incliné est m g cos.
Et, comme je l'ai montré, cos = sin  (angles complémentaires).
C'est ainsi que l'on obtient m g sin.

Mais l'angle que j'ai ajouté sur le schéma en violet est égal à (angles alternes-internes). Donc on peut utiliser le côté opposé et on trouve m g sin. C'est effectivement une autre façon de faire...

Si je comprend bien il y'a plusieurs façon de faire ?

Oui, si on veut mais ce n'est pas vraiment différent...
En principe, la projection d'un vecteur sur un axe se fait par l'intermédiaire du cosinus de l'angle. En l'occurrence, comme il s'agit d'angles complémentaires, l'un des cosinus se transforme en sinus (pour tout exprimer en fonction du même angle).

C'est le b-a  ba  de la mécanique du plan incliné. Ce sera toujours comme ça. Il y aura toujours des projections à faire sur des axes pour pouvoir additionner les forces de façon simple (ce sont des vecteurs).
Donc il est absolument nécessaire de maîtriser ces histoires de projection (qui sont simples d'ailleurs ! ).

j'aurai une question svp le côté adjacent est bien mg cos sur le schéma  ?

Le côté adjacent pour l'angle est bien mgcos