Inscription / Connexion Nouveau Sujet
DYNAMIQUE: mouvement d'un palet sur une table à coussin d'air
Bonjour, j'ai besoin d'aide sur cet exercice. Je n'arrive pas à trouver les coordonnées du vecteur poids dans le repère choisi par l'énoncé. Donc je n'arrive à répondre à aucune question...
Données: g = 10 m.s^-2 ; α = 10° ; β = 50°
Sur une table à coussin d'air inclinée d'un angle α par rapport au plan horizontal, on étudie le mouvement d'un palet.
A la date t = 0, on lance, avec une vitesse à partir du point O, le palet vers le haut dans le plan de la table.
On étudie le mouvement du centre d'inertie G de la table dans le plan rapporté au repère (O,i;j).
L'axe (Oy) qui porte le vecteur unitaire j est donc parallèle à la ligne de plus grande pente du plan incliné.
1) Etablir l'équation du mouvement du centre d'inertie G du palet.
2) Etablir l'équation cartésienne de la trajectoire décrite par le centre d'inertie G du palet dans le repère (O,i,j). Quelle est sa nature ?
3) Donner en fonction de α, β,g et Vo l'expression de l'ordonnée maximale Ymax atteinte par le centre d'inertie G du palet dans le plan (O, x, y).
La mesure de l'ordonnée maximale donne Ymax= 80 cm. Calculer la valeur de la vitesse initiale Vo du palet

Bonsoir
Un peu comme d'habitude en mécanique : le système étudié étant le palet, il faut faire l'inventaire des forces extérieures puis appliquer la relation fondamentale de la dynamique pour obtenir l'expression du vecteur accélération de G.
Tu va alors tomber sur une étude très proche de celle du mouvement parabolique dans un plan vertical du centre d'une balle lancée avec une vitesse initiale de vecteur incliné de l'angle  par rapport à l'horizontale.
par rapport à l'horizontale.
Je te laisse réfléchir et proposer une solution.
système: palet
Référentiel terrestre supposé Galiléen
Bilan de forces: : poids du palet
: réaction normale de la table
TCI: +
=m
et
dans le repère
suivant l'axe (Ox) on a: Px= max
suivant l'axe (Oy) on a: Py=may
et je boque là, je ne sais pas comment déterminer les coordonnée de
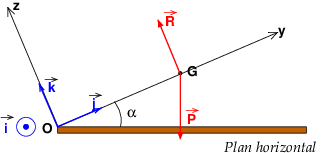
Pour mieux t'aider dans ta projection de la relation fondamentale de la dynamique, voici un schéma avec pour plan de figure le plan (Oyz), l'axe (Ox) étant perpendiculaire à ce plan et orienté vers l'avant.
A noter que, puisque G reste dans le plan (Pxy) :
z=0  t
t
vz=dz/dt=0  t
t
az=dvz/dt=0  t.
t.
donc si je comprends bien
donc
Equation horaire du mouvement(t)
si j'ai trouvé l'équation horaire alors je pe"ux faire le reste facilement
Est-ce juste?


