Inscription / Connexion Nouveau Sujet
Dynamique de rotation 6
Bonjour, aidez-moi svp à corriger cet exercice.
Problème : Un cylindre de rayon R, mobile autour de son axe de révolution (
) horizontal est solidaire d'une tige AB rigide de masse négligeable, fixée sur un diamètre du cylindre. Le milieu de la tige coïncide avec le centre du cylindre. Le moment d'inertie du cylindre par rapport à l'axe () est J1 = 4,0.10-2 kg.m².
On donne : AB = 1 m ; R = 10 cm.
D'accord, mais mon problème est que la masse du cylindre n'est pas donnée, puisque pour répondre à la 1ère question je dois appliquer le Théorème de l'accélération angulaire au système.
OK je vois !
1) Calculons l'accélération angulaire du cylindre
- système : cylindre + les deux masselottes A et B ;
- référentiel : terrestre (supposé galiléen) ;
- bilan des forces :
• le poids de la masse A ;
• le poids de la masse B ;
• le poids du cylindre ;
• la force appliquée en D ;
• la réaction de l'axe
sur le cylindre.
(Voir schéma ci-haut)
Le Théorème de l'accélération angulaire :
= J1.
"
Mais la somme des moments de P1 et P2 est nulle, le moment de la réaction est nul, le moment du poids du cylindre est aussi nul.
Donc le Théorème de l'accélération angulaire devient :
F.r = J1." 
" = (F.r)/J1
AN :
Ce n'est pas J1 qui intervient mais le moment d'inertie du solide en rotation. Il faut tenir compte des masses en A et B.
Oh je vois, merci !
Je reprend à partir du Théorème de l'accélération angulaire :
= J." 
F.R = J."
Mais J = J1 + 2.m1(AB/2)² = 9.10-2 kg.m²
AN :
2.a) Déterminons la valeur de la masse M
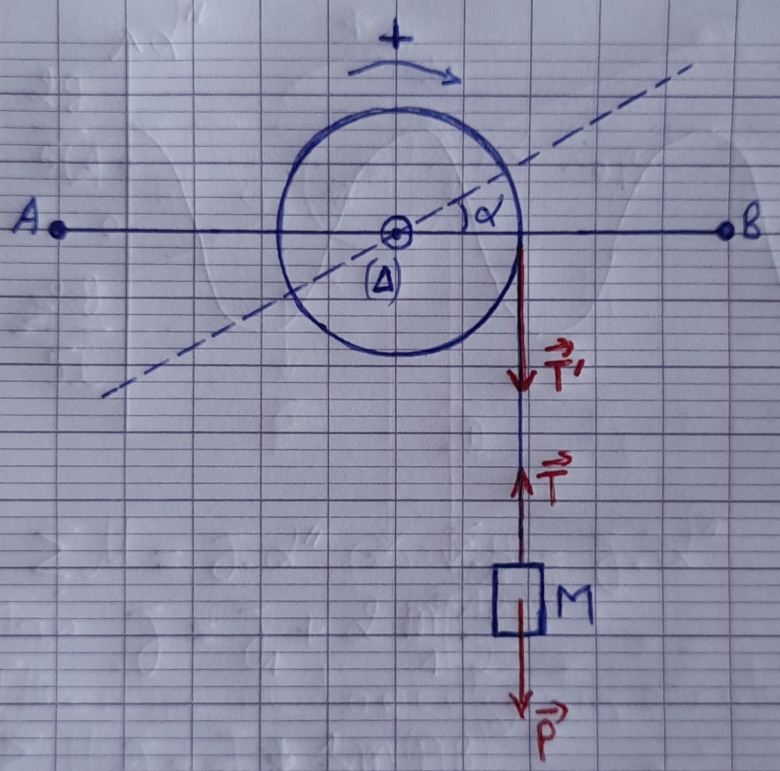
• Sur le solide en rotation : = J."
Donc T'R = J." (1)
• Sur la masse M en translation :
Suivant le sens du mouvement on a :
P - T = Ma T = M(g - a) (2)
D'après le principe des actions réciproques T = T'
Alors
Or a = R."
D'où
AN : M = 0,45 kg
(2d/a)
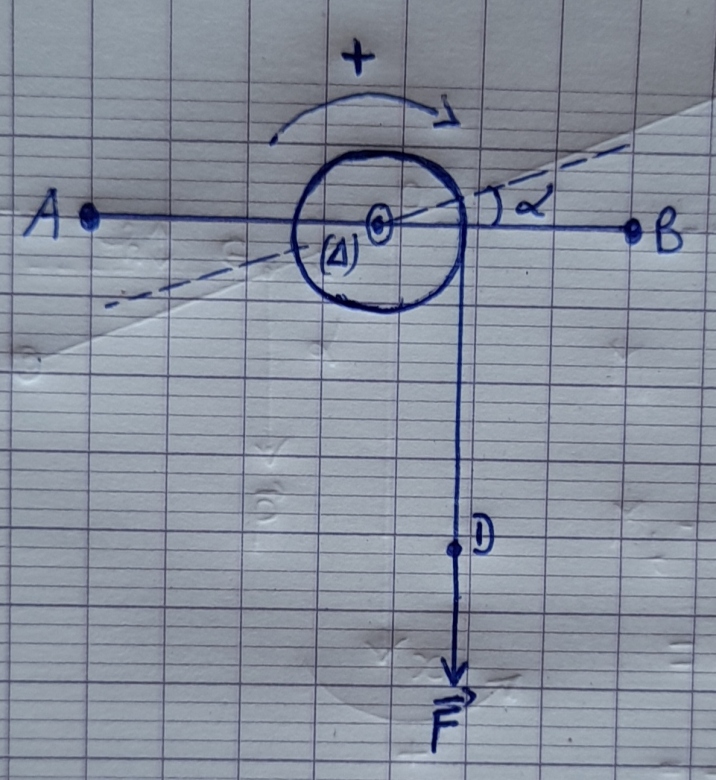
3) Calcul du moment du couple
La nouvelle accélération angulaire est
Ainsi le moment du couple est C = J.''
AN : C = - 1,19 N.m
Question 3 : à ce que je comprends, l'accélération est la même qu'aux questions précédentes.Il faut juste utiliser une masse plus importante pour compenser l'action des frottements.
Donc si je comprend bien, le bilan des forces doit changer....
Le Théorème de l'accélération angulaire donne
AN : c = - 0,276 N.m
Ah d'accord, je vois !
En posant T = T' puis en tirant le moment du couple, j'obtiens :
c = J." - M2R(g - R.")
AN : C = - 0,156 N.m
C'est bon ?
Annuler
connectez vous