Inscription / Connexion Nouveau Sujet
Dynamique
Bonsoir j'ai besoin d'aide sur la dernière question 1-e) de l'exo merci.
Exercice
Un jeu consiste à lancer un solide (S) de masse m = 50 g à partir d'un point A pour qu'il heurte un solide (S')
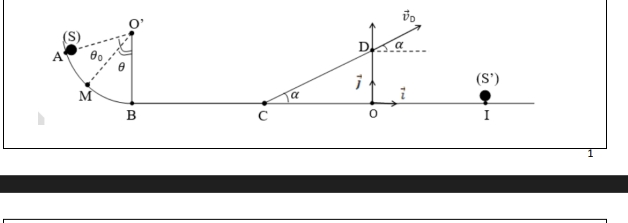
placé en I. Le dispositif de jeu est représenté par la figure ci-dessous constitué par une piste ABCD :
- AB est un arc de cercle parfaitement lisse de centre O' et de rayon r = O'A= O'B = 90 cm
et tel que (𝐴O'B ) = 𝜃o = 72° ;
- BC est une piste rectiligne de longueur ℓ1 = 10 cm ;
- CD est une piste rectiligne de longueur ℓ2 = 15 cm inclinée d'un angle 𝛼 = 30 ° par rapport à l'horizontale ;Ton ami qui participe au jeu, lance le solide en A avec une vitesse initiale 𝑣A = 7 m.s-1. Le solide arrive à un point
M défini par l'angle (𝑀O'𝐵) = 𝜃.
Le solide (S) aborde la partie BC avec la vitesse 𝑣B = 7,8 m.s-1, les frottements sont assimilables à une force
constante 𝑓 et opposée au mouvement. La vitesse acquise en C est 𝑣C = 6 m.s-1.
Le solide (S) quitte la piste au point D avec la vitesse 𝑣D = 2,7 m.s-1.
Tu es sollicité pour étudier le mouvement du solide sur les différents trajets. On prendra g = 9,8 m.s-2.
1) Mouvement sur AB
a) Enoncer le théorème de l'énergie cinétique.
b) Etablir l'expression de la vitesse 𝑣M en fonction de 𝑣A, g, r, 𝜃 et 𝜃0.
c) Vérifier que 𝑣B =7,8 m.s-1.
d) Montrer que la réaction en M peut se mettre sous la forme 𝑅 = 𝑚𝑔 (3𝑐𝑜𝑠𝜃 − 2𝑐𝑜𝑠𝜃0 +
𝑣𝐴
2
𝑟𝑔)
e) En quel point la réaction est - elle maximale ? Calculer 𝑅𝑚𝑎𝑥.
Bonjour,
Il faut calculer R en chaque point et chercher le maxi.
Par contre, quand je dis calculer, il n'est pas nécessaire de faire le calcul explicite, il faut :
- poser le calcul
- traduire par un schéma dans les trois zones
- la conclusion à la lecture du schéma devrait être facile.
Bonjour,
L'énoncé n'est pas complet.
La partie écrite des questions concerne uniquement le mouvement sur AB
et donc la question "e) En quel point la réaction est - elle maximale ? Calculer 𝑅𝑚𝑎𝑥." concerne seulement le parcours sur l'arc AB
En 1d, l'énoncé donne l'expression de la réaction qu'on doit trouver.
A partir de là (donc après avoir trouvé cette expression) qui écrite correctement est : 𝑅 = 𝑚𝑔 (3𝑐𝑜𝑠𝜃 − 2𝑐𝑜𝑠𝜃0 + 𝑣𝐴²/(rg))
Il suffit de trouver l'angle 𝜃 qui rend R maximum et en déduire la valeur de Rmax.
Bonsoir Candide et pourquoi on doit seulement trouver l'angle 𝜃 qui rend R maximum et non les deux ?
Bonsoir,
Presque yout est imposé (m , g , vA, r, 𝜃o), seul 𝜃 varie.
De plus, 𝜃 varie dans [𝜃o ; 0].
Il y a, dans le cas de cet exercice, une et une seule valeur de 𝜃 qui rend R maximum... c'est immédiat à trouver par un simple coup d'oeil sur la relation donnée de R.
Bonjour,
Hors sujet, quoique ...
Je n'aime pas les énoncés qui ont l'air de poser des problèmes pratiques mais utilisent des données complètement hors de la normale.
Un exemple ici (entre d'autres), si on calcule la force de frottement sur le tronçon BC, on trouve |f| = 6,21 N … ce qui correspondrait à un coefficient de frottement de 6,21/(0,05*9,8) = 12,7 (arrondi). Ce n'est pas ce qu'on peut appeler une valeur raisonnable pour ce type de problème.
Ce n'est pas ainsi qu'on permettra aux élèves et étudiants d'acquérir un bon "feeling" pratique ou un bon esprit critique.