Inscription / Connexion Nouveau Sujet
Dynamique
bonjour. Je rencontre un serieux probleme pour resoudre un exercice; Merci davance pour votre aide
voici lenonce
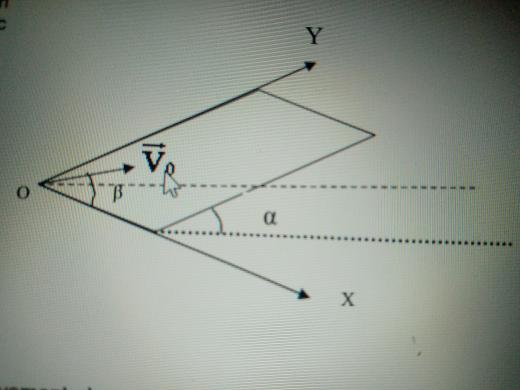
Une table à coussin d'air est inclinée d‘un angle α par rapport au plan horizontal. Depuis un coin inférieur de la table, on lance en
translation vers le haut un palet de masse m, avec une vitesse V0
parallèle au plan de la table. Le vecteur vitesse V0 fait un angle β avec l'axe horizontal OX situé dans le plan de la table, et donc
un angle (
/2)
avec l'axe OY. Le point O est la position initiale du centre d'inertie G du palet.
Le palet se déplace sans frottement sur la table.
On étudie le mouvement du point G dans le repère
orthonormé (O, ), l'axe OY qui porte le vecteur
unitaire j est donc parallèle à la ligne de plus
grande pente du plan incliné .
3.1 Etablir les équations horaires x(t) et y(t) du mouvement du centre d'inertie G du palet.
3.2 Ecrire l'équation cartésienne de la trajectoire du centre d'inertie du palet.
3.3 Montrer que la coordonnée y reprend la même valeur pour deux valeurs différentes de t. et préciser
à quelle condition.
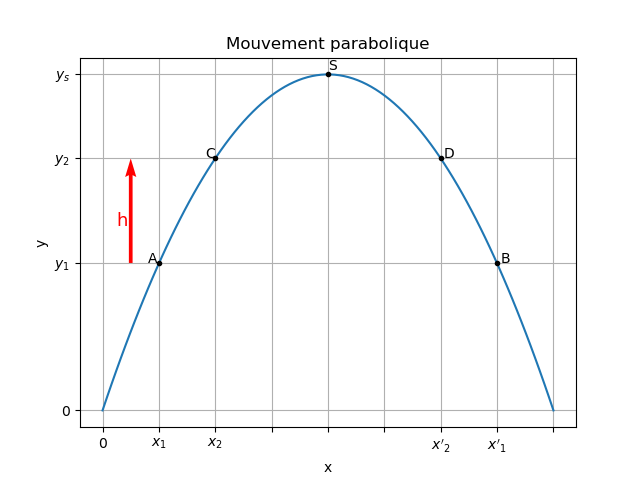
3.4 On considère deux couples de points (A,B) et (C,D) de la même trajectoire du centre d‘inertie ; les
ponts A et B ont la même ordonnée y1 ; les points C et D ont la même ordonnée y2.
On pose h = y2 - y1 (avec y2 > y1). Soit T1 l'intervalle de temps séparant les dates de passage par A
et B et T2 l'intervalle de temps séparant les dates de passage par C et D. Etablir la relation existant
entre α, h , T1,T2 et g (intensité de pesanteur).. Calculer l'angle α.
Application numérique : h =13 cm ; T1= 0,80 s ; T2 = 0,2 s ; g =10 SI.
vu qu'on est dans le repère (o i j)
déjà je ne vois pas comment je pourrais projeter le vecteur accélération suivant cette axe
Bonjour
Applique la relation fondamentale de la dynamique au solide. Tu devrais montrer assez facilement que l'accélération de G est un vecteur constant, ce qui te ramène à un problème classique déjà étudié.
Pour mieux voir tu peux faire une figure avec comme plan de figure un plan vertical contenant l'axe (O,y), plan perpendiculaire donc à l'axe (O,x).
Nos messages se sont croisés. Tu as bien lu mes deux derniers messages ?
L'existence du coussin d'air rend les frottements négligeables. On peut donc considérer la réaction de la table inclinée perpendiculaire au plan de cette table.
OKOK
je rectifie alors
P_vect+R_vect=ma_vect
a la projection
ax=0 ay=-gsin
et suivant k c une constante ?
Le point G se déplace nécessairement dans le plan (O,x,y) parallèle à la table puisque la distance de G au plan de la table est fixe. Tu as nécessairement :
az = 0
D'accord avec toi pour ax et ay.
D accord je vois
Vx=Vocos
Vy=-g sint+Vosin
x=Vocost
y=-(1/2)gsint2+Vosint
2-y=-(1/2)(gsinx2)/(Vo2cos2)+tanx
3-lorque y=0, t=0 et t= (2Vo2cos2)/gsin
OK jusqu'à 3.2.
Pour 3.3, en notant S le sommet de la trajectoire, il faut montrer que pour y<yS, existent deux valeurs possibles différentes de t. Tu fais le calcul uniquement dans le cas y=0.
Oui, je me suis dit que cela ne pourrait arriver que dans le cas où y=0 vu que la trajectoire est parabolique
du coup j'ai trouvé les deux t mentionnés en haut
Imagine la trajectoire parabolique de sommet S puis imagine le tracé d'une droite horizontale d'ordonnée y positive mais inférieure à ys. Cette horizontale coupe la trajectoire en deux points d'abscisses x1 et x2 correspondant à deux dates de passage t1 et t2. On pose T=t2-t1 et on s'intéresse à deux valeurs différentes de y...
ahhh d'accord je vois mieux maintenant
y=-(1/2)(gsinx)/(Vocos2)+tanx
On pourrait étudier la fonction en posant f(x)=y, même je trouve que le fait que ca soit une l'équation dune parabole devrait suffir comme justification si je me trompe pas
Sur un sujet original comme celui-ci, le plus sage consiste à suivre pas à pas les consignes de l'énoncé.
D accord, c est noté
y=-(1/2)(gsinx)/(Vocos2)+tanx
On a l'équation d une parabole alors pour Y
Ys la cordonnées Y prend deux valeurs à différents valeurs de t
c est suffisant ?
3.3. Tu n'as pas bien compris mon message du 19-05-24 à 21:21.
Cette intersection de deux points entre la trajectoire parabolique et une horizontale d'ordonnée y n'existe que si y<ys et je pense qu'il faut ici déterminer l'expression de ys.
3.4. Tu peux raisonner directement sur les équations horaires sans passer par celle de la trajectoire.
Les dates de passage à une ordonnée y1 sont les deux racines t1 et t'1 de l'équation :
et on demande la différence : T1=t'1-t1
puis on demande de refaire un calcul analogue pour une ordonnée :
y2 = y1 + h.
Je vois.
3.3) pour ymax => Vy=0
alors je sort le "t" et je le remplace dans y pour trouver ymax
Ymax=(Vo2sin2)/(2gsin)
Alors pour y<ymax, un même y admet deux t différents
Annuler
connectez vous