Inscription / Connexion Nouveau Sujet
Dynamique
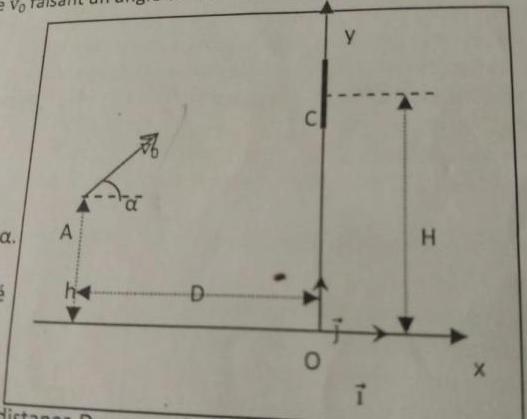
On étudie les tirs de basket-ball de manière simplifiée. On suppose que le joueur est face au panneau à une distance D de ce dernier. Le cercle du panier est situé à une hauteur H = 3,05 m au-dessus du sol et on assimilera le cercle au point C situé sur le panneau. De même, le ballon sera considéré comme ponctuel. On néglige les frottements fluides de l'air. A l'instant
t = Os, le joueur tire le ballon d'un point A situé à
une hauteur h = 2,00 m au-dessus du sol en imposant une vitesse vo faisant un angle a avec l'horizontale (voir figure ci-contre). Le mouvement sera étudié dans le repère (O, i, j).
On prendra g = 10 m.s2.
1°) Etablir les équations horaires du mouvement du ballon dans
le repère (O, i, j).
2°) En déduire l'équation cartésienne de sa trajectoire.
3°) On suppose que le module de la vitesse initiale est fixé.
Déterminer l'équation à vérifier par l'angle a pour que le panier soit marqué (le ballon passe par le ballon C). On mettra cette équation sous la forme d'une équation du second degré en tan alpha.
4°) Montrer que cette équation n'admet des solutions que si le module vo de la vitesse initiale vérifie une inéquation du second degré en vo au carré
5°) En déduire l'existence d'une valeur minimale Vomin de Vo pour que le panier soit marqué.
6°) Les règles de la Fédération Internationale de Basket-ball fixent la distance D pour un lancer-franc et un panier à trois points. Calculer Vomin:
6-1) pour un lancer franc, la distance D vaut alors 4,60 m;
6-2) pour un panier à trois points, la distance D vaut 6,25 m.
7) Si la condition précédente (en 4°) est vérifiée, donner l'expression de tan a et en déduire qu'il existe deux angles possibles pour marquer le panier.
8) Calculer les valeurs des deux angles a permettant de marquer un lancer-franc en supposant que vo= 10,0 m.s1.
9) Pour un angle de tir fixé a = 70°, trouver la valeur de vo de la vitesse initiale pour marquer le panier par un lancer-franc.
Bonjour. Je fais cette exercice et je rencontre qlq difficultés, je suis bloqué à la question 4
Voici ce que j'ai essayé de faire
1) Équations horaires
vect a=>ax=0 et ay=-g
vect V=>Vx=Vo cos
et Vy=-gt+Vo sin
vect OM=>x=(Vo cos)t-D et y=-(1/2)gt²+(Vo sin)t+h
2) Équation de la trajectoire
y= (-g/(2Vo² cos²))x²+(tan-gD/(Vo²cos²)x+Dtan+h-gD²/(2Vo²cos²)
3)pour l'équation j'ai trouvé
(-gD²/2Vo²)tan² + Dtan + h-(gD²/2Vo²)-H=0
Pour la question 4, j'obtiens cela:
(2g/Vo²)(h-H-(gD²/2Vo²))
1
Sauf que je ne vois pas trop comment continuer pour obtenir avec vo une inéquation du second degré
bonsoir,
Pour la question 4:
(2g/Vo²)(h-H-(gD²/2Vo²)) >= 1
<=> h-H-(gD²/2Vo²) >= Vo²/(2g) car Vo²/(2g)>0
et en multipliant parVo² des deux côtés on devrait trouver ce qui est demandé
Non pas en Vo, mais c'en est une en Vo2, ou encore une équation bicarrée
Montrer que cette équation n'admet des solutions que si le module vo de la vitesse initiale vérifie une inéquation du second degré en vo au carré
Vo⁴/2g
Bonjour,
Tu écris :
"On a du coup (-Vo⁴/2g)+Vo²(h-H)-(gD²/2)<= 0"
Vérifie, si il n'y aurait pas une erreur de signe.
Bonsoir à tous,
Comme l'a souligné Candide, il y a un pb de signe dans ton expression.
5) une fois que l'on a trouvé l'inéquation du type: aX2+ bX +c >= 0 (en posant X=Vo2)
il faut étudier le signe du trinôme et en déduire Vomin
Bonjour,
Tu écris :
"On a du coup (-Vo⁴/2g)+Vo²(h-H)-(gD²/2)<= 0"
Vérifie, si il n'y aurait pas une erreur de signe.
Je reprend du coup
Delta = D² -4(-gD²/2Vo²)(h-H-(gD²/2Vo²))
On pose: Delta
0
Alors D²-4(-gD²/2Vo²)(h-H-(gD²/2Vo²))
0
En simplifiant j'obtiens
1+4(g/2Vo²)(h-H-(gD²/2Vo²))
0
4(g/2Vo²)(h-H-(gD²/2Vo²))
-1
h-H-(gD²/2Vo²)
-Vo²/2g
En multipliant par Vo²
Vo⁴/2g+Vo²(h-H)-(gD²/2)
05)Pour déduire ducoup je pose Vomin⁴/2g+Vomin²(h-H)-(gD²/2)=0
Delta = (h-H)²+4(1/2g)(gD²/2)>0
Donc Vomin existe
6)1-pour un lancer franc avec D=4,60m
Vomin²= 57,7m/s² => Vomin= 7,6m/s
6)2- pour un panier a trois points avec D=6,25m
Vomin²=73,9m/s² => Vomin= 8,6m/s
Bonjour,
Les valeurs numériques sont bonnes.
MAIS attention aux unités.
Tu écris par exemple : Vomin²= 57,7m/s²
L'unité est fausse. l'unité de V² est m²/s², le m/s² est une unité d'accélération et pas une unité de vitesse qu carré.
Annuler
connectez vous