Inscription / Connexion Nouveau Sujet
DM sur le mouvement
Bonjour, je n'arrive pas à faire ces questions. J'aimerais avoir de l'aide s'il vous plaît. Merci d'avance ce qui vont répondre.
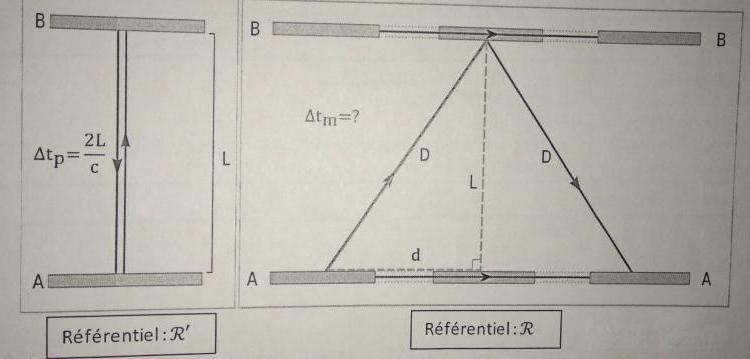
Soit une lumière se réfléchissant sur deux miroirs A et B situé dans une fusée se déplaçant à une vitesse v.
1) Exprimer la durée ∆tm en fonction D et c.
2) Exprimer la distance d en fonction de la vitesse v de la fusée et la durée ∆tm.
3) En déduire une expression de ∆tm en fonction de L, c et v.
4) Retrouver la relation : ∆tm = (1)/√(1-(v2)/(c2))×∆tp.
Pour répondre ces questions, je vous met une photo des figures du deux miroirs A et B.
Bonsoir,
Les questions 1) et 2) qui sont simplissimes sont à la portée d'un élève de 3ème.
Elles sont destinées à te guider pour la suite qui est un peu plus difficile.
On attend tes propositions.
OK pour la 1)
∆tm = 2D/c
donc D = c*∆tm / 2
Pour la 2) j'ai obtenu
∆tm = 2d/v
donc d= v*∆tm / 2
Il te faut ensuite appliquer le théorème de Pythagore :
D² = L² + d²
puis remplacer D et d par leurs expression tirées des questions 1 et 2
La suite est plus de la cuisine algébrique que de la physique.
Penser aussi à introduire au moment opportun : L = ∆tp / 2
Oh d'accord merci. J'ai essayer de le faire mais je ne sais pas si c'est bon.
D2= L2+d2
 ((c×∆tm)/2)2= L2+((v×∆tm)/2)2
((c×∆tm)/2)2= L2+((v×∆tm)/2)2
 (c2×∆tm2)/22 = L2+ (v2×∆tm2) /22
(c2×∆tm2)/22 = L2+ (v2×∆tm2) /22
 (c2)/2= (∆tp)/2+ (v2)/2
(c2)/2= (∆tp)/2+ (v2)/2
 (c2)/2= ∆tp+(v2)/2
(c2)/2= ∆tp+(v2)/2
 c2=∆tp+ v2
c2=∆tp+ v2
Un simple coup d'il sur la dernière ligne de ton calcul suffit pour voir qu'il est faux.
En effet il y figure la somme d'une durée Δtp avec le carré d'une vitesse.
C'est un peu comme si on additionnait des navets et des carottes !
Je reprends :
Dans mon post du 24-02-20 à 21:09 dernière ligne :
Lire : Penser aussi à introduire au moment opportun 2L / c =  tp
tp
à la place de L = ∆tp / 2
Ah c'est comme ça qu'il faut faire ! Merci  mais enfaite nous sommes en quel question ? Parce que j'ai l'impression on a trouver en même temps la réponse du question 4).
mais enfaite nous sommes en quel question ? Parce que j'ai l'impression on a trouver en même temps la réponse du question 4).
C'est exact !
Les questions 1, 2, 3 sont des questions destinées à te guider pour obtenir le résultat de la question 4
En plus de la question 4, mon post répond au passage à la question 3 obtenu à la ligne 3 du calcul :
On peut alors en remplaçant 2L par c *  tp mener le calcul d'une manière légèrement différente pour obtenir le résultat de la question 4
tp mener le calcul d'une manière légèrement différente pour obtenir le résultat de la question 4


