Inscription / Connexion Nouveau Sujet
DM physique spé
Bonsoir,
je dois rendre ce dm dans 3 jours et je le trouve long et assez difficile , pourriez vous m'aider

1)Écrire l'expression littéraLe du volume V de la corde, en fonction de son diamètre d et de
sa longueur L.
2) Écrire l'expression littérale de la masse m de la corde en fonction de sa masse volumique
p et de son volume V.
3) À patir des deux questions précédentes, calculer la masse m de la corde n'6, en
détaillant les étapes du calcul.
4) Calculer la masse des autres cordes et remplir la quatrième ligne du tableau ci-dessus. Le
détail des calculs n est pas exigé.
5) Calculer la masse linéique p de la corde n'6, en détaillant les étapes du calcul.
6) Calculer la masse linéique des autres cordes et remplir la cinquième ligne du tableau ci dessus.
Le détail des calculs n est pas exigé
7) Rédiger une phrase pour expliquer en quoi les valeurs numériques de f1 et p présentes
dans le tableau ci-dessus sont cohérentes avec la formule littérale de f1 donnée plus haut.
Au bout du manche de la guitare, les cordes sont enroulées et fixées autour de clefs.
Lorsque !'on tourne la clef dans un sens, on tire sur la corde. Lorsque l'on tourne la clef dans
l'autre sens. on détend la corde.
Le rôle des clefs est d'accorder l'instrument, pour que chaque corde vibre exactement à la
fréquence souhaitée. En effet, si la température de la pièce augmente, la masse volumique
des cardes diminue et entraîne une variation de f1.
8) indiquer quelle grandeur physique de la corde est modifiée lorsque l'on tourne la clef
d'une corde.
9) En étudiant l'expression littérale de f1, indiquer dans quel sens varie f1 lorsque la
température augmente. Expliquer le raisonnement suivi.
1o) On indique que la masse linéique m de la corde n'6 vaut p = 7,68.10puissance-3 kg.m . Calculer
la valeur de la tension T à appliquer sur cette corde pour que f1 soit égale à 82,4 Hz.
J'en suis a la question 3 merci.
Bonjour,
L'énoncé n'est pas complet. Il faut tout recopier si tu veux de l'aide.
Quelles sont tes réponses aux trois premières questions ?
L'unité de masse linéique n'est pas kg.m mais est kg.m-1
Je prépare le tableau pour la suite :
| Corde n° | 6 (mi1) | 5 (la1) | 4 (ré2) | 3 (sol2) | 2 (si2) | 1 (mi3) |
| Fréquence f1 (Hz) | 82,4 | 110 | 147 | 196 | 246 | 330 |
| Diamètre d (mm) | 1,12 | 0,89 | 0,70 | 0,55 | 0,35 | 0,25 |
| Masse m (kg) | ||||||
Masse linéique  (kg.m-1) (kg.m-1) |

Ce que tu proposes pour la première question est faux.
À la condition que V soit le volume, d le diamètre et L la longueur de la corde.
Mais j'attends toujours que tu complètes l'énoncé. Il manque des données.

Ah oui:
Une guitare classique comporte six cordes métalliques de longueur de vibration L égale(L= 63,0 cm) et de masse volumique p égale (p = 7800 kg.m puissance-3). Chacune de ces cordes a été
choisie et positionnée de tel sorte que sa fréquence fondamentale de résonance f1
(fréquence pour laquelle on observe un seul fuseau) ait une valeur bien précise

Comment peux-tu imaginer que l'on puisse résoudre un exercice si l'énoncé est incomplet ?
_________
Comment calcule-t-on le volume d'un cylindre de diamètre d et de longueur L ?

L'énoncé demande l'expression littérale du volume V en fonction du diamètre d et de la longueur L
V =  .R2.L
.R2.L
et comme
R = d/2
V =  (d2/4).L
(d2/4).L
Que proposes-tu pour la deuxième question ?

Oui.
Je suppose que la masse volumique est plutôt représentée (c'est conventionnel) par la lettre grecque  ("rho")
("rho")
donc : m =  .V
.V
m sera exprimée en kilogramme (symbole kg)
si
la masse volumique  est exprimée en kg.m-3
est exprimée en kg.m-3
et le volume V en m3
_________
Quel est le détail de ton calcul pour la masse de la corde n° 6 ?

Pour la corde n°6;
V=
 1,12-4²/4
1,12-4²/4 63.10-3
63.10-3
V=3,14 3,1.10-9
3,1.10-9 63.10-3
63.10-3
V= 6,2.10-10m3
m=7800 6,2.10-10
6,2.10-10
m=4,8.10-6 kg
Il y a une erreur d'un coefficient mille dans le volume (et donc dans la masse)
Peux-tu recommencer le calcul du volume en faisant très attention aux puissances ?

Exact !
D'où m = 7 800  6,2.10-7
6,2.10-7  4,84.10-3 kg
4,84.10-3 kg
Soit environ 4,8 grammes
| Corde n° | 6 (mi1) | 5 (la1) | 4 (ré2) | 3 (sol2) | 2 (si2) | 1 (mi3) |
| Fréquence f1 (Hz) | 82,4 | 110 | 147 | 196 | 246 | 330 |
| Diamètre d (mm) | 1,12 | 0,89 | 0,70 | 0,55 | 0,35 | 0,25 |
| Masse m (kg) | 4,84.10-3 | |||||
Masse linéique  (kg.m-1) (kg.m-1) |
Alors, quelles valeurs pour terminer cette ligne ? (Si tu sais utiliser un tableur, c'est le moment ! )

Eh bien, j'attends :
. les valeurs pour la question 4
. le détail du calcul et le résultat pour la question 5
. les valeurs pour la question 6

4) corde 5: m=3,06.10-3
corde 4 m=1,89.10-3
corde 3 m=6,67.10-4
corde 2 m= 4,72.10-4
corde 1 m = 2,41.10-4
5) =m/L
=m/L
donc pour la corde n°6
 =4,84.10-3/63.10-2 = 7,68.10-3 kg.m-1
=4,84.10-3/63.10-2 = 7,68.10-3 kg.m-1
6) corde 5: =4,86.10-3
=4,86.10-3
corde 4:  =3.10-3
=3.10-3
corde 3:  = 1,06.10-3
= 1,06.10-3
corde 2 :  =7,49.10-4
=7,49.10-4
corde 1 :  =2,82.10-4
=2,82.10-4
Je reprends les valeurs avec lesquelles je suis d'accord :
| Corde n° | 6 (mi1) | 5 (la1) | 4 (ré2) | 3 (sol2) | 2 (si2) | 1 (mi3) |
| Fréquence f1 (Hz) | 82,4 | 110 | 147 | 196 | 246 | 330 |
| Diamètre d (mm) | 1,12 | 0,89 | 0,70 | 0,55 | 0,35 | 0,25 |
| Masse m (kg) | 4,84.10-3 | 3,06.10-3 | 1,89.10-3 | 4,73.10-4 | 2,41.10-4 | |
Masse linéique  (kg.m-1) (kg.m-1) | 7,68.10-3 | 4,85.10-3 | 3,00.10-3 | 7,50.10-4 |
Voilà ; il y a donc trois "trous". Peux-tu vérifier tes calculs ?

| Corde n° | 6 (mi1) | 5 (la1) | 4 (ré2) | 3 (sol2) | 2 (si2) | 1 (mi3) |
| Fréquence f1 (Hz) | 82,4 | 110 | 147 | 196 | 246 | 330 |
| Diamètre d (mm) | 1,12 | 0,89 | 0,70 | 0,55 | 0,35 | 0,25 |
| Masse m (kg) | 4,84.10-3 | 3,06.10-3 | 1,89.10-3 | 1,17.10-3 | 4,73.10-4 | 2,41.10-4 |
Masse linéique  (kg.m-1) (kg.m-1) | 7,68.10-3 | 4,85.10-3 | 3,00.10-3 | 1,85.10-3 | 7,50.10-4 | 3,83.10-4 |
Mes calculs sont faits au tableur. Je n'arrondis pas les résultats intermédiaires mais seulement les résultats finals (d'où les quelques écarts avec tes résultats).
Ton énoncé est si mal recopié que je ne vois pas quelle réponse donner aux questions suivantes.
Il serait bon d'avoir un énoncé correctement recopié...

Une guitare classique comporte six cordes métalliques de longueur de vibration L égale(L= 63,0 cm) et de masse volumique  égale (
égale ( = 7800 kg.m puissance-3). Chacune de ces cordes a été
= 7800 kg.m puissance-3). Chacune de ces cordes a été
choisie et positionnée de tel sorte que sa fréquence fondamentale de résonance f1 (fréquence pour laquelle on observe un seul fuseau) ait une valeur bien précise.
On indique que:
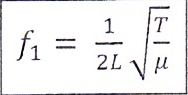
avec L ; longueur de la corde(m)
T: force de tension de la corde(N)
m: masse de la corde
 : masse lineique de la corde
: masse lineique de la corde
Voilà... enfin !
Que proposes-tu pour la réponse à la question 7 ?
Je peux te dire ce que j'ai fait : j'ai calculé la valeur de T pour toutes les cordes (la question 10 te demande ce calcul pour la corde n° 6) ; de l'utilité d'un tableur...

On verra cela à la question 10.
Pour le moment, tu peux faire l'hypothèse que les cordes sont soumises à peu près à la même tension T (même s'il est prudent pour les cordes très fines de ne pas appliquer une tension trop élevée...).
En considérant le tableau, tout particulièrement les valeurs de f1 et celles de  y a-t-il cohérence ?
y a-t-il cohérence ?

Les valeurs de f et celles de  sont cohérentes car comme
sont cohérentes car comme  se trouve au dénominateur plus sa valeur augmente plus la frequence diminue.
se trouve au dénominateur plus sa valeur augmente plus la frequence diminue.
8) C'est la force de tension de la corde qui est modifiée.
9) Lorsque la température augmente la masse volumique diminue donc la masse m de la corde aussi donc 
diminue et comme il est au dénominateur f1 augmente.
10) la force de tension vaut a peu prés 65,7 N
11)C'est la longueur de la corde
12)La longueur diminue diminue donc f1 augmente
13) c'est 82,4 Hz car plus la fréquence est basse plus le son est grave.
Est-ce que c'est juste?
Question 8 : D'accord
Question 9 : Pas d'accord.
L'énoncé est pour le moins bizarre.
Lorsque la température augmente, la dilatation augmente la masse volumique, bon, on peut voir les choses ainsi.
La masse ne change pas !
En revanche la longueur augmente par la dilatation. Donc la tension de la corde diminue. (le L avec lequel ont été faits les calculs est la distance entre les extrémités de la corde qui est imposée par la géométrie de la guitare. Cette distance ne change guère avec la température).
La tension diminue et donc la fréquence baisse.
Enfin, c'est mon point de vue...
Question 10
Je ne trouve pas cette valeur de l'intensité de la tension.
Peux-tu indiquer le détail de ton calcul ?
Je ne connais pas les questions 11 à 13 (et au-delà ? ) Tu ne les as pas recopiées.

11)Indiquer quelle grandeur physique de la corde est modifiée lorsqu'on immobilise l'extrémité de la corde entre deux frettes du manche
12) indiquer comment varie le fréquence f1 de la corde lorsqu'on effectue cette opération
13) donner la valeur de la fréquence correspondant au son le plus grave qu'une guitare puisse émettre justifier
Pour la question 10 j'ai fait;
T=F²x(2L)²x
T=82,4² (2
(2 63,0.10-2)²
63,0.10-2)² 7,68.10-3
7,68.10-3
T=82,78 N
Je m'étais trompé 
Bonus... (ce n'est pas demandé par ton énoncé) :
| Corde n° | 6 (mi1) | 5 (la1) | 4 (ré2) | 3 (sol2) | 2 (si2) | 1 (mi3) |
| Fréquence f1 (Hz) | 82,4 | 110 | 147 | 196 | 246 | 330 |
| Diamètre d (mm) | 1,12 | 0,89 | 0,70 | 0,55 | 0,35 | 0,25 |
| Masse m (kg) | 4,84.10-3 | 3,06.10-3 | 1,89.10-3 | 1,17.10-3 | 4,73.10-4 | 2,41.10-4 |
Masse linéique  (kg.m-1) (kg.m-1) | 7,68.10-3 | 4,85.10-3 | 3,00.10-3 | 1,85.10-3 | 7,50.10-4 | 3,83.10-4 |
| Tension de la corde (N) | 82,8 | 93,2 | 103 | 113 | 72,1 | 66,2 |
Question 11
Oui, la longueur (il y a aussi le risque de modifier un peu la tension)
Question 12
Oui, la fréquence augmente et la note jouée est donc un peu plus haute (plus aiguë) ; c'est ainsi que l'on pourra jouer toutes les notes situées entre les notes de deux cordes "à vide"
Question 13
Exact. C'est la corde de masse linéique la plus forte et elle n'est pas très tendue. Il n'y a qu'un seul fuseau et on ne la raccourcit pas en plaçant le doigt entre deux frettes. Donc c'est la note de la corde "à vide" (mi1), dont la fréquence vaut environ 82,4 Hz
_____________
Il me semble que cet exercice est fini.
S'il y a un autre exercice dans le même DM il doit être posté dans un nouveau topic.
C'est seulement si cet exercice-ci se continuait (questions 14, 15, etc.) qu'il faudrait poster à la suite.

La caisse de resonnance
Sur une guitare, la carde qui est pincée est la source sonore. Elle produit un son de
fréquence fondamentale f1 précise, accompagnée de ses harmoniques. Mais son diamètre
est si petit qu'elle vibre très inefficacement dans l'air et le son en est pratiquement inaudible.
C'est pourquoi les cordes sont couplées via le chevalet â la caisse de résonance, dont la
large surface supérieure va vibrer beaucoup plus efficacement dans I' air et créer un son
audible. Le volume intérieur de la caisse de résonance va contribuer à donner au son produit
un timbre unique.
14) En modélisant les molécules constituant l'air par de petites sphères, illustrer par un schéma le rôle de la caisse de résonance, en dessinant les molécules d'air déplacées par les vibrations d'une corde seule, et par celles d'une corde reliée à une caisse
de résonance.
15) Rédiger un court paragraphe expliquant pourquoi deux guitares dont les caisses de
résonance ont une forme différente (ou bien sont faites d'un bois différent) possèdent un
timbre différent. Vous pourrez, dans ce paragraphe, exploiter les notions de « réflexion », de
« transmission » et d' « absorption » d'une onde sonore.
Froduction de notes de musique
L'oreille est sensible au rapport entre les fréquences de deux notes jouées simultanément.
Les instruments de musique et les morceaux de musique sont donc Créés de telle sorte que
les sons produits soient harmonieux entre eux. lls appartiennent à ce qu'on appelle une« gamme ».
une gamme est une succession de notes (c'est à-dire de sons) dont les fréquences sont
reliées entre elles de manière bien définie. En Europe, on a introduit la « gamme tempérée »
pour faire de la musique. La gamme tempérée comporte 12 sons successifs, nommés : do,
do dièse, ré, ré dièse, mi, fa, fa dièse, sol ,sol dièse, la, la dièse, si. Dans cette gamme,
« l'intervalle » entre deux sons est toujours le même.
L'intervalle entre deux sons est le quotient de la fréquence du son le plus aigu par celle du
son, le plus grave. Dans la gamme tempérée, l'intervalle entre deux sons (deux « notes »)
successifs est constant. égal à 22/12
Arrivé à la note « si 1 » de la première gamme (gamme 1), on recommence une autre
gamme (gamme 2), plus aigue (do 2, do 2 dièse .).
Le tableau ci-dessous regroupe les fréquences des notes des deux premières gammes
il me manque le tableau
17) On étudie la corde n 1. lndiquer le numéro de la frette juste avant laquelle il faut
appuyer pour obtenir un « la 3 ». Justifier la réponse.
18) Calculer la fréquence f1 ( la 3) associée à la note « la 3 », en détaillant les étapes du calcul.
19) lndiquer comment faire, en pinçant deux cordes en même temps, pour produire
simultanément un « la 2 dièse » et un « mi 2)
On, suppose que pour la guitare étudiée, lorsque le guitariste joue un « ré 2 » avec une
intensité sonore I, alors les harmoniques 1 et 3 sont émis aussi. Le premier harmonique est
émis avec une intensité sonore l/2, et le troisième harmonique est émis avec une intensité
sonore 1/3.
20) Tracer le spectre du son global émis (intensité sonore en fonction de la fréquence).
Pourriez vous m'aider?



