Inscription / Connexion Nouveau Sujet
DM Physique Le Grand Huit
Bonjours, j'ai beaucoup de problème à mo nsujet de physique. J'ai cherché de l'aide sur google et je ne trouve pas le sujet. Deuxièment personne à compris au sujet alors je me suis dit avec l'aide du forum je pourrais réussir. Voici le sujet
Le grand Huit :
Dans tout l'exercice, on prendra g=9.81 N/kg.
Le grand huit est un manège classique des parcs d'attractions. Son principe est simple, faire monter mécaniquement un wagonnet à une certaine altitude puis se servir de l'énergie potentielle ainsi acquise pour parcourir un rail ayant un profil varié.
Dans cet exercice, nous allons étudier trois phrases du mouvement du wagonnet :
- Phase de montée
- phase de descente avec un looping
- phase d'arrêt
Partie I : Phase de montée
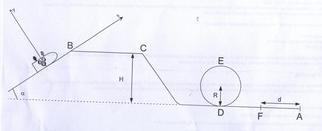
Un wagonnet de masse m=500 kg se déplace sur la partie rectiligne AB du rail, incliné d'un angle = 35.0°. I lest entraîné par un cable à la vistesse constante V(AB) = 10.0 km/h. Le câble exerce une force T, constante, parallèle aux rails. Le contact entre le wagonnet et les rails se fait sans frottement. AB = 60.0 m
1. Faire un bilan des forces exercées sur le wagonnet
Ici j'ai mis le Poids (P), La tension du Cable ( T) et La réaction au support (R)
2. Quelle est la relation entre ces forces ? justifiez
d'après la loi de newton W(P)+W(T)+W(R) = 0
les forces doivent former un dynamique fermé
3. Quelle relation existe-t-il entre la somme des travaux de ces forces le long du déplacement AB ?
1/2 . m . V ² = W ( P ) + W ( R ) + W ( T )
4. Exprimer, en fonction des données du texte, le travail de chacun de ces forces
W ( P ) = m . g . (Longeur x sin ( alpha ) )
W ( R ) = 0 car il est perpendiculaire au wagonnet
W ( T ) = - W ( P )
Donc W ( Force ) = F x Longeur AB x cos ( alpha )
5. En déduire l'expression littérale de la valeur de la force de traction du câble
Alors là, je sais pas quoi mettre
6. Calculez cette valeur
Là je suppose qu'il faut que je répond à la question 5 d'abord.
7. Calculez la puissance de la tension du câble le long du déplacement AB
Je n'arrive pas
la partie II :
a. Conservation de l'énergie mécanique
8. Exprimez littéralement l'énergie mécanique du wagonnet en C puis en F. On prendra la référence de l'énergie potentielle de pesenteur au niveau du tronçon DF
9. Montrer que l'énergie mécanique du wagonnet se conserve le long du tronçon CF
pour que le wagonnet puisse parcourir le looping, il faut que sa vitesse E soit égale ) V e = Racine de G.R ou R est le rayon du cercle
10 . Montrez que la hauteur H minimal pour le wagonnet puisse parcourir le looping est égale à H = 34.4 m
dans la suite de l'exercice on considère que cette condition est vérifiée, c'est à dire que l'on prend H = 34.4 m
b. Calculs de quelques vitesses et hauteurs
11. Calculez la Vitesse Vd atteinte oar le wagonnet en arrivant au point D avant de parcourir le looping
12. Quelle est la vitesse du wagonnet au point F ? vous ne ferez pas de calcul mais vous justifierez soigneusement la réponse
Partie III :
En arrivant au point F de la trajectoire, le wagonnet possède une vitesse V(F) = 26.0 m.s-1. Arrivé à ce point, le contact avec les rails se fait avec une force de frottement constante f jusqu'à l'arrêt total du wagonnet au point A. Cette force de frottement a pour valeur f = 6300 N
a. Calcul de la distance d'arrêt
13. Enoncez le théorème de l'énergie cinétique
14. Calculez la distance d'arrêt d= FA du wagonnet
b. Calcul de la puissance de la force de frottement
on note x la distance parcourue à partir du point F. Une étude approfondie montre que cette distance parcourue dépend du temps suivant la fonction :
x(t) = - f/2m . t² + V(f).t il apparit effectivement qu'a t=0 la distance parcourue est nulle.
15. calcuez le temps qu'a duré le freinage jusqu'a l'immobilisation totale du wagonnet
16. En déduire la puissance de la force de frottement durant cette phase
Merci de bien vouloir m'aider
Bonsoir,
1) OK
2) parce que la vitesse est constante
3) OK
4) Le travail du poids est résistant. Il n'y a que la composante parallèle à la pente qui travaille (l'autre est perpendiculaire au déplacement)
WP = - m g sin(
) AB
On a :
WT = T AB
ça va jusque là ?...
Pour la 5
On a WT + WP = 
Ec = 0 ==> WT = -WP ==> T = m g sin
Pour la 6
Il faut faire le calcul
Pour la 7
WT = T AB
La puissance est PT = WT / t.
t = AB / v = 60 / (10000/3600) = 21,6 s
Partie II
a) Em = Ec + Ep = 
W(F)
8) Em(C) - Em(B) = 0 ==> Em(C) = Em(B)
(entre B et C, aucune force ne travaille)
Em(B) - Em(A) = Ec(B) - Ec(A) + Ep(B) - Ep(A) = mgH
Em(F) - Em(C) = 0 ==> Ec(F) - Ec(C) + Ep(F) - Ep(C) = Ec(F) - Ec(C) - m g H
Ec(C) = Ec(B) = (1/2) mvAB2
Ec(F) - (1/2) mvAB2 - m g H = 0
Ec(F) = (1/2) mvAB2 + m g H
Et : Ec(F) = (1/2) mvF2
9) Pas de frottement et pas d'autre force que le poids donc l'énergie mécanique se conserve.
9. Montrer que l'énergie mécanique du wagonnet se conserve le long du tronçon CF
pour que le wagonnet puisse parcourir le looping, il faut que sa vitesse E soit égale ) V e = Racine de G.R ou R est le rayon du cercle
10 . Montrez que la hauteur H minimal pour le wagonnet puisse parcourir le looping est égale à H = 34.4 m
Ce n'est pas clair... La ligne du milieu est rattachée à quoi ?
non c'est pour la semaine mais j'essaye de bien comprendre, j'essaye de bien analysé et je te re-mercie beaucoup
pour que le wagonnet puisse parcourir le looping, il faut que sa vitesse E soit égale ) V e = Racine de G.R ou R est le rayon du cercle
Faut-il le démontrer ?
10)
Em(D) - Em(C) = 0 ==> Em(D) = Em(C)
==> Ec(D) + Ep(D) = Ec(C) + Ep(C)
==> (1/2)mvD2 = (1/2)mvC2 + mgH
==> vD2 = vC2 + 2gH
Em(E) - Em(D) = 0 ==> Em(E) = Em(D)
==> Ec(E) + Ep(E) = Ec(D) + Ep(D)
==> (1/2)mvE2 + mg(2R) = (1/2)mvD2 = (1/2)mvC2 + mgH
==> vE2 = vC2 - 4gR + 2gH
On doit avoir vE 
(gR) ==> vE2 gR
Donc : vC2 - 4gR + 2gH gR
2gH gR + 4gR - vC2
H (5/2)R - (vC2/2g)
Vérifie les calculs... J'ai peut-être fait une erreur...
H (5/2)13,75 - ((10000/3600)2/(2*9,81))
H 33,98 m
Essaie de comprendre ça ... Je ne trouve pas 34,4 m. Pour trouver 34,4, il faudrait que le rayon R soit égal à 13,92 m.
Vérifie les calculs... J'ai peut-être fait une erreur...
j'ai fait différement. mon calcul est
Em(C) = Em(E)
Ec(C) + Ep(C) = Ec (E) + Ep (E)
0 + m.g.h = 1/2 . m . V² + m . g . z
h = 1/2 . m . V ² + m . g . z / m . g
h = 1/2 x 500 x (9.81x13.75)² + 500 x 9.81 x 13.75 x 2 / 500 x 9.81
h = 34.37 mètre
donc H = 34.4 mètre minimal
par contre pour la vitesse D j'ai du mal j'ai fait Ec (c) + Ep (C) = Ec (D) + Ep (D)
1/2 m . V(c)² + m . g .h = 1/2. m V(D) ² + m . g .h mais après je ne sais pas s'il faut divisé ou faire comme une équation
Quant à ton calcul, c'est bien parce que tu trouves 34,4...
Mais un détail me gêne.
Si Ec(C) = 0, ça veut dire que vC = 0.
Or, la vitesse est la même en B et en C (Em constante, Ep est la même donc Ec est la même donc la vitesse est la même).
Donc si la vitesse est nulle entre B et C, comment fait-il pour aller de B à C ?
Si , le temps de freinage est obtenu pour x(t) = d.
Equation du second degré qui permet de trouver t
De B à C, on a Em = 0 (aucune force ne travaille de B à C parce qu'elles sont toutes perpendiculaires au déplacement).
Donc Em(C) = Em(B).
L'énergie potentielle est la même puisque B et C sont à la même hauteur.
Donc vC = vB.
Or vB = 10 km/h par hypothèse...
oui j'ai mis car d'après l'énergie mécanique la vitesse reste la même c'est à dire constante du début du trajet jusqu'au looping puis à la fin du looping jusqu'à F c'est ça,
Annuler
connectez vous