t1 = 0 -> D1 = 10,2
t2 = 0,29 -> D2 = 13,2

en t1:
R1 = Delta D/Delta t = (13,2 - 10,2)/(0,29 - 0) = 10,3448276
R2 = (13,2-10,2)/10,2 = 0,29411765
R3 = (13,2-10,2)/(10,2.(0,29-0)) = 1,01419878
---
t2 = 0,29 -> D2 = 13,2
t3 = 0,57 -> D2 = 16,8

en t2:
R1 = Delta D/Delta t = (16,8 - 13,2)/(0,57 - 0,29) = 12,8571429
R2 = (16,8-13,2)/13,2 = 0,27272727
R3 = (16,8-13,2)/(13,2.(0,57-0,29)) = 0,97402597
---
etc ...

-----
Sauf distraction.  

Merci bcp pr l'aide dsl ms je n'ai pas pu venir plutot

Bonjour
J'ai a nouveau des difficultés :s

C'est toujours le meme exercice
-A partir du rapport dont les valeurs diffrents le moins, justifier ce qui conduit les biologistes a considerer que la densité peut etre reprsentée par une fction derivable D qui verifie D'(t)= K x D(t) avec D' la derivée de D et K une constante a derteminer numeriquement.Il faut donc une equation ki presente a la fois la fonction et sa derivée(Utilistation de la fonction Exponentielle).

Aide(Je n'ai pas su repondre a cette kestion.)

2- On admet l'existence de la seule fonction definie et derivable sur l'ensemble des réels qui verifie ,
Pour tout x  : f'(x) = f(x) et f(0)=1  [c'est la fonction exponentielle]
But : avec Excel trouvons une approche graphique de la courbe representative de cette fonction.

Justifier que pour a réel et h proche de 0 on ait:
f(a + h) (1 + h)f(a)
Ma Reponse :

On sait ke f'(a) = f(a) or  
f'(a) = Lim h=>0 [f(a+h) - f(a)]/h
f'(a) [f(a+h) - f(a)]/h
f'(a)h f(a+h) - f(a)
f'(a)h + f(a) f(a+h)
f(a)h + f(a) f(a+h) (car f'(a) = f(a))
(1+h)f(a) f(a+h)  

c'est bien ca?

-justifier que pour tout n les valeurs approché de f(nh) onbtenue à l'aide de cette méthode sont les termes d'une suite GEOMETRIQUE de raison (1+h)

???Ma reponse :
f(nh)=?
donc f((n+1)h) = f(nh +h) = f(nh)(n+h) ??
apres je sais pas donc voila si vous pouvez m'aide ce serait bien parce ke sans ca je ne pe pas faire la suite.
Merci .....

Help me

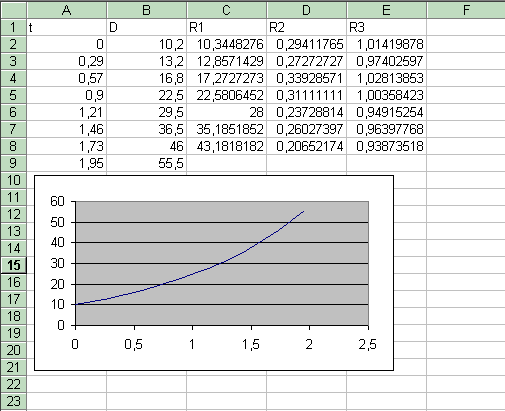
Le tableau excel de JP suggère que R3 est ( à peu près ) constant
C'est à dire que delta D / (D x delta t)= K  constante

soit delta D/delta t = K * D

Or pour delta t infiniment petit ( à la limite quand il tend vers 0 )

delta D/delta t = D'(t)

( voir ce que tu écris : f'(a) = Lim h=>0 [f(a+h) - f(a)]/h )

Ainsi, la colonne de R3 suggère que

D'(t)= k * D ( t) ,  K constante

ici K semble être égal à 1 ( ou un peu moins , voir la colonne R3 )

Pour la suite ta démo est un peu longue mais correcte

pour la dernière question :

on utilise f ( a + h )=env ( 1 + h ) f ( a )
d'abord avec a = 1
f( 1 + h) =env ( 1 + h ) f ( 1 )
ensuite on écrit
f( 1 + 2h )= f ( (1 + h) + h )
maintenant avec a = 1 + h  on obtient
f( 1 + 2h )=env  ( 1 + h )f ( 1 + h )
on remplace f(1+h) par la première approximation et on obtient        
f( 1 + 2h )=env ( 1 + h )( 1 + h ) f ( 1 )
D'où f( 1 + 2h )= env ( 1 + h )² * f ( 1 )

puis  f ( 1 + 3h) =env f ( (1+2h) + h )
                  =env ( 1 + h ) f ( 1 + 2h)
                  =env ( 1 + h )( 1 + h )² f ( 1 )
                  =env ( 1 + h )^3 . f ( 1 )

etc (récurrence)

f(1+nh) =env  (1+h )^n . f(1 )

les valeurs approché de f(1+nh) [ et pas f(nh) comme tu l'écris ] obtenues à l'aide de cette méthode sont les termes d'une suite GEOMETRIQUE de raison (1+h) et de premier terme f(1).

Merci bcp pour votre mais pour la derniere kestion ke g poster c'est bien ecrit : les valeurs approché de f(nh) onbtenue à l'aide de cette méthode sont les termes d'une suite GEOMETRIQUE de raison (1+h)
A moins ki ai erreur d'ennoncé de la part du prof ....En tout grace a votre aide je pense ke je pourrais faire un grand pas du moins j'espere.
Mais est-ce ke l'on peut dire :
f(nh) =env  (1+h )^n-1 . f(1 )???

Help me msieur Zlurg !!!

Bonsoir
Y a t-il kelk'un ki pourrait m'aider?

Slt n'y a t-il personne ki puisse m'aider un plus c ke c pr demain le DM :p