Inscription / Connexion Nouveau Sujet
dm de physique 1ere S
Le sujet de cet exercice est : TRAJECTOIRE PARABOLIQUE
On enregistre la trajectoire d'un mobile autoporteur à "coussin d'air" de masse M = 605 g , lancé sur une table plane inclinée d'un angle a = 8° par rapport à l'horizontale . L'intervalle de temps entre 2 positions est de 60 ms .
La valeur de la réaction est R = 5,9N
Alors je dois répondre à 2 questions qui sont :
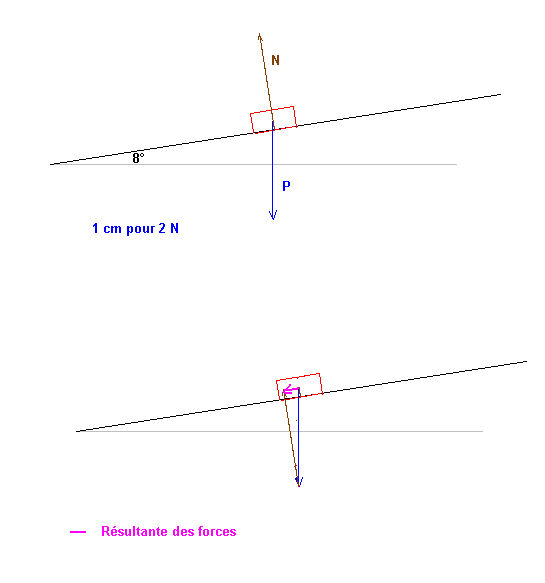
1° Faire une vue de profil de la table et du mobile .
Représenter les forces qui s'appliquent sur le mobile au cours de son mouvement et je dois préciser l'échelle que j'ai choisie .
2° Par une construction graphique montrer que la somme des forces appliquées a même direction que la ligne de plus grande pente du plan incliné .
Et ces questions je ne vois pas comment faire et comment commencer
(je n'arrive jamais à faire un dessin de profil c'est pour ça )
quelqu'un pourrait -il m'aider à commencer à faire cet exo
et me l'expliquer merci
Bonjour quand même...
Il doit bien y avoir des dessins avec vues de profil : creuse un peu ! 
![]() [lien]
[lien]

Oui désolé Bonjour
excusez moi de cette petite maladresse
j'ai regardé ce que tu me proposait
mais je comprends quelles sont ces forces c'est : P er R C'est ça
mais pour la question 2 je ne comprend pas du tout
pourriz vous m'aider merci
bonsoir je vous remercie de m'avoir répondue
et je voudrai savoir su le premier dessin si cela ne vous dérange pas :
N c'est quoi c'est la normal ?
et ce premier dessin c'est en fait la première question ?
Pourquoi on ne représente pas R ?
et le deuxième dessin c'est la deuxième question en fait ?
et si je devrai représenter les vecteurs (delta V avec une flèche sur V)3 et (delta V avec une flèche dessus )je dois tracer le vecteur vitesse ç ça avant
mais je ne vois pas la suite
est ce quelqu'un pourrait m'aider encore un petit peu
merci d'avance
Oui, vieille habitude chez moi de noter N la réaction normale du support (qui ici est aussi la réaction complète si on néglige les frottements)
N est R dans le cas de l'exercice.
delta V / delta t est l'accélération et est dans la direction et le sens de la résultante (en mauve sur le dessin du bas).

bonsoir et merci de m'avoir répondu mais je ne comprends pas delta V / delta t
et pouvez vous m'aider à la 3ème question si je devrai représente delta vg dite précedemment
merci de me répondre et de votre grande patience
Bonjour jean-michou,
Bonjour et merci à J-P pour ces schémas 
Je voulais laisser J-P te répondre. En son absence (temporaire...) :
On note souvent le vecteur qui représente la variation (représentée par le
 ) de la vitesse au point 3
) de la vitesse au point 3
Cette variation de vitesse est approximativement égale à la différence de la vitesse au point 4 (la vitesse est modélisée par un vecteur) et de la vitesse au point 2
On obtient donc en première approximation cette évolution de la vitesse en retranchant (vectoriellement) le vecteur du vecteur
Ceci montre comment la vitesse a varié pendant l'intervalle de temps  t autour du point 3. Cet intervalle de temps est lui-même égal à t4 - t2
t autour du point 3. Cet intervalle de temps est lui-même égal à t4 - t2
différence entre les instants de passage aux points 4 et 2
Comme te le montre le dessin de J-P en construisant tous les vecteurs on constate qu'ils sont tous dirigés selon la ligne de plus grande pente du plan incliné et tous orientés vers le bas de cette ligne.
C'est une conséquence de la seconde loi de Newton : le vecteur variation de vitesse (on l'appelle le vecteur accélération) est proportionnel au vecteur résultante de toutes les forces.

bonsoir,
j'ai eu le même exercice à faire et il y a un truc que je ne comprend pas : c'est quoi la ligne de plus grande pente du plan incliné ? Oo
si quelqu'un comprend ce terme, en le remerciant ^^
Si tu places une bille sur un plan incliné et que tu la lâches, elle va descendre suivant la ligne de plus grande pente et pas par un autre chemin.
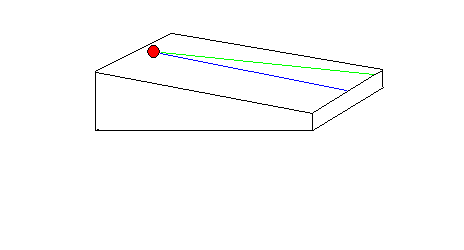
Sur le dessin (en perspective).
Si tu lâche la bille rouge, elle va descendre suivant la ligne bleue et pas par exemple par la ligne verte ou une autre.
Les 2 lignes (la bleue et la verte) sont droites, mais la ligne verte est plus longue, "elle descend moins fort" que la ligne bleue.
En partant de l'endroit où est la bille rouge, le chemin bleu est celui "qui descend le plus fort", c'est la ligne de plus grande pente en partant de l'endroit indiqué.
OK ?