Voici une figure :



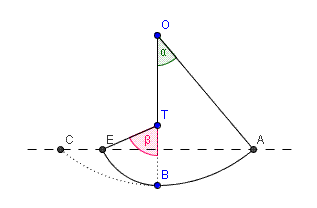
Le point O est le point d'attache du pendule
Le point A est le point de départ et l'angle = 40° (l'angle vert)
Le point B est le point bas

En l'absence de la tige T le mobile remonterait en C

Mais il y a la tige en T
Donc le mobile remonte en E

On te demande la mesure de l'angle (l'angle rouge)

Tu es sur que = 40 car dans l'énoncé, c'est 45°.

4/ Em = ec+epp
ec1(a)=1/2*0.8/0 = 0J
ec2(e)=1/2*m*v²
epp1(a)=m*g*z(a) = m*g*l[1-cos]
epp2(e)=m*g*z(e) = m*g*d[0.4-cos]

ec1+epp1=ec2+epp2
1/2*m*v²+m*g*z(a)=1/2*m*v²+m*g*z(e)
m*g*l[1-cos]=1/2*m*v²+m*g*d[0.4-cos]
g*l[1-cos]=1/2*v²+g*d[0.4-cos]
2g*l[1-cos]=1/2*v²+2g*d[0.4-cos]
2*9.8*1[1-cos45]=2*9.8*0.6[0.4-cos]+5.74  (v²= réponse2?)
5.74=19.6*0.6(0.4-cos)+5.74
5.74=4.704-5.88cos+5.74
5.88cos=5.74-5.74+4.704
5.88cos=4.704
cos=4.704/5.88
cos=36.9°

C'est ça?

Merci à l'avance.

Non, ce n'est pas du tout cela.

C'est bien d'avoir vu l'erreur ; donc l'angle rouge vaut 45° et non pas 40°

Que vaut la distance TE ?
A quelle hauteur se situe le point T au-dessus du niveau des points C, E et A ?

Quelle est donc la valeur de l'angle ?

La, vraiment je n'ai aucune idée.

Que vaut OA ? OB ? OT+TE ?
Que vaut OT ?
Que vaut donc TB ou TE ?

Quelle est la distance entre O et le plan horizontal P passant par A, E et C ?
Quelle est la distance entre le plan P et T ?

Conclusion...

OA= 1.00m
OB= 1.00m
OT+TE = 0.6m+0.4m = 1.00m
OT=0.6m
TB=TE=0.4m

OA=OE=OC=1.00m

Quelle est la distance entre le plan P et T ? : je ne sais pas.

Est-ce que c'est ça?

La distance entre le plan horizontal qui passe par les points A, E et C et le point bas, B est connue depuis le message du 17/02 à 13 h 36

z = L[1 - cos()]c'est ça?

Mais je ne vois vraiment pas je rapport avec la solution.

Svp, explique-moi pour raisonnement.

Merci à l'avance.

La distance entre le plan P (plan horizontal passant par A, E et C) et B est

L[1 - cos()]

Tu connais la distance TB
Donc... tu connais la distance de T au plan P

Comme tu connais aussi TE, il me semble que le calcul de est immédiat...

TB = 0.4m
la distance de T au plan P est d[0.4-cos]

C'est ça?

TB = 0,40 m : exact !

Je ne comprends pas la deuxième ligne ; utilise l'"Aperçu" avant de poster pour vérifier ce que tu as écrit.

Désolée, j'ai mis la distance de T au plan P est d[0.4-cos]

C'est faux.

On utilise cette distance depuis le 17 février vers 13 h 00 ! Alors tu devrais savoir la calculer depuis...

Je ne comprends plus rien.
0.4[d-cos]alors?

La distance du plan P au point B est L[1 - cos(] = 1[1 - cos(45)] = 0,293 m environ

La distance de T à B est 0,40 m

Donc la distance de T au plan P est 0,107 m

La longueur de TE est 0,40 m

Que vaut l'angle ?

d[0.6-cos]=0.107
0.4(0.6-cos)=0.107
0.24-0.4cos=0.107
0.24-0.107=0.4cos
0.133=0.4cos
0.133/0.4=cos
0.3325=cos
= 70.6°

C'est pas ça? ça ne semble beaucoup.

SVP, merci à l'avance.

C'est faux.

Je t'avais expliqué comment faire le 21/02 à 11 h 18 :

= cos^-1(0,107 / 0,40) 74,5°

Bonsoir.
J'ai lu votre convesation, et il se trouve que jujee et moi avons le même DM à faire.C'est exactement le même énoncé. Votre conversation m'a permis de comprendre beaucoup de chose sur ce chapître (nous n'avons pas fini la leçon et ce DM nous a été donné avant les vacances sans explications).
Le fait est que je comprend pas du tout la démarche à adopter pour la question 4.ALors si cela ne vous embéte pas j'aimerais que vous m'expliquer (je ne veut pas les réponses, mais juste comprendre la démarche, etc).

Je vous rappelle la question:
4/On place, sur la verticale de o, à la distance d=60.0cm, une tige métallique T sur laquelle le fil du pendule, lâché comme précedemment (m=45°), vient buter.
En admettant que le choc du fils du pendule sur la tige T, s'effectue sans perte du d'energie, déterminer l'angle dont le pendule remonte aprés le choc avec la tige.

Merci à l'avance de votre aide.

Bonsoir f0fi

La seule chose à comprendre pour la question 4 est que la boule remonte toujours au même niveau qui est celui du départ, s'il n'y a pas de frottement.

Donc :
. en l'absence de tige, la boule remonte en C (ma figure le 20/02 à 13 h 21)
. avec la tige, la boule remonte sur un arc de cercle de centre T et jusqu'en E

Ensuite, c'est un peu de géométrie pour mesurer les longueurs concernées et en déduire la valeur de l'angle

On doit calculer:
OT et TB ? c'est cela?

Mais part contre j'aimerais avoir des pistes pour calculer s'il vous plait.

OB = 1 mètre, c'est l'énoncé, il n'y a rien à calculer.
OT = 0,60 m = 60 cm c'est encore l'énoncé et il n'y a toujours rien à calculer.
TB = 1 - 0,60 = 0,40 m = 40 cm
Ce calcul n'est pas surhumain

oui c'est vrai que ce n'est pas surhumain

Pour je pensait utilisé le cosinus mais il faudrait utiliser la droite passant par C, E et A. non?

Appelons P le point d'intersection de la droite OTB et du plan horizontal passant par A, E et C

cos() = TP / TE

on connais TE. Pour TP, on ne connais pas sa situation , enfin je veut dire qu'on a rien indiquant sa position ... peut tu me donné une piste? merci

On connaît OA
On connaît

Que vaut OP ?

sin= OP/OA
sin 40° = OP/1
OP= 0.64  

c'est bon?

Tu confonds le cosinus et le sinus

D'autre part la valeur de l'angle dans l'énoncé est 45° et non pas 40°
Tu as mal lu le topic.

ah oui effectivement sin = opposé/ hypothénuse et cos= adjacent / hypothènuse

donc, cos = OP/OA
cos 40° = OP/1
OP= 0.76 cm

c'est correct maintenant?

oh donc
cos = OP /OA
cos 45°= OP/1
OP = 0.70cm

Oui, OP = 70,7 cm

Donc TP = 10,7 cm (voir le message du 21/02 à 11 h 18)

Tu confonds aussi les mètres et les centimètres

OP = 0,707 m c'est-à-dire 70,7 cm

oui ... .

donc il faut calculer EP.
Donc, OC= 100cm
OP= 70,7 cm

Admettons que l'angle COP= '.
alors, sin'= CP / CO
cos 45 = CP/ 1
CP= 70.7 cm

mais j'ai l'impression que ce calcul n'a servit à rien ...

tu aurais une indication? je trouve pas ...

on cherche EB ou EP.
c'est ça?

Lis, dans cet ordre, les messages du 22/02 à 20 h 31 puis à 07 h 55

mais nous ne connaissons pas EP ...
par quel moyen pouvons nous le calculer?

Comme on n'a pas besoin de le calculer, peu importe.

cos = TP / TE
= cos ^-1 ( TP/TE )
= cos ^-1(10.7/40)
= cos ^-1* 0,26)
= 74.48°

c'est bon?

  c'est bon ou non?

La réponse se trouve dans mon message du 22/02 à 07 h 55

donc je pense avoir termniné... Je vous remercie beaucoup !
à bientot

Je t'en prie.
A une prochaine fois !

merci beaucoup Coll pour toute l'aide que tu m'a apporté ( un peu en retard, désolée)
j'ai réussit à comprendre cette leçon et en partie grâce à tes explications (car les explications de notre prof ne sont pas claires)
Merci beaucoup encore une fois.

Dommage... aide-toi de ton livre ! Ils sont souvent très bien faits.