Inscription / Connexion Nouveau Sujet
DM de "Maths", Circuit éléctrique et les resistances
Bonjour !
J'ai eu l'occasion de travailler (obligatoirement ^^') sur un DM de "Maths" qui fait reference à la physique, que je n'arrive pas à resoudre correctement :s.
Voilà l'enonce :
[/b]En Physique : Circuits équivalents[b]
En série
___[ R1 ] ___ [ R2 ]____ (Ceci represente les resistance placées en
série ! )
Resistance equivalente R
telle que R = R1 + R2
En parallele
___[ R1 ]___ (Ceci represente les resistances placées en ___/ \____ parallèle)
\___[ R2 ]___/
Resistance equivalente R
telle que 1= 1 + 1
R R1 R2
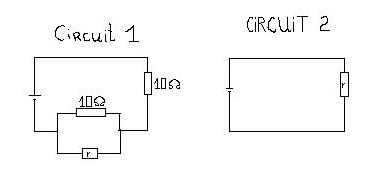
Voila les 2 circuits suivants :
questions:
a) Déterminer r pour que les deux circuits soient équivalents(on arrondira au dixième).
b) Déterminer r pour que la resistance équivalente du circuit 1 soit superieure à celle du circuit 2.
Pour la question a j'ai fait des essais mais je n'arrive pas plus loin, et je ne suis pas sûr, si je me dirige vers la bonne reponse.
Voilà ce qu j'ai fait :
Si les circuits sont equivalents alors on aura
(1/r + 1/10) + 10 = r
soit
(1/r + 1/10) + 10 = r
on reduit au même denominateur
(10/10r + r/10r) + 10 = r
((10+r)/10r + 10) - r = 0
((10+r)/10r + 100/10) - r/1 = 0
on ouvre les parenthèses ?
(10+r)/10r + 100/10 - r/1 = 0
on met tout au même denominateur
(10+r)/10r + 100r/10r - 10r²/10r = 0
Je ne vois pas comment aller plus loin ni d'ailleurs comment faire la question b)
Aidez moi s'il vous plaît
Merci d'avance 
Voilà j'crois avoir résolu cet exercice, veuillez me dire si ce que j'ai fais est correct, (j'aurai plutôt mi cet exercice dans la section mathématique...)
Voilà ce que j'ai trouvé:
J'appelle R1 le 1er circuit
J'appelle R2 le 2e circuit,
R1= 1/R + 10 = 1/10 + 1/r + 10
R2= r
On veut trouver R1=R2
1/10+1/r+10=r
1/10+1/r+10-r=0
là je met tout sur le même dénominateur:
(r+10+100r-10r²)/10r=0
(-10r²+101r+10)/10r=0
j'enlève le dénominateur:
-10r²+101r+10=0
après j'ai fais la forme canonique, et je trouve x1= -0.1 et x2= 10.2,
alors je garde que le 10.2 car une intensité de résistance ne peut être négative.
Après pour vérifier mon résultat j'ai fais R1= 1/10+1/r+10, et j'ai remplacé r par 10.2 et au final je trouve donc 10.2 en arrondissant au dixième comme c'est écrit dans l'énoncé,
10.2 est aussi le résultat de R2, car R2=r,
donc je pense avoir trouvé, voilà
Bonsoir,
R1 = 10 +
R1 = 10 +
R1 = r
10 + = r
= r - 10
10r = (r-10)(r+10)
10r = r2 + 102
r2 - 10r - 100 = 0
r = 5 + 5
5
r = 16,18033989 
16,2
Ah ouai ok merci daniel62,
mais pour le b), comment tu fais pour trouver r, qui fait le résultat de R1 supérieur à R2, là vraiment je sais pas...
f(r) = r2 - 10r - 100
s'annule pour r=5-55 (à rejeter) et r=5+55 (16,2)
admet un minimum pour r=5 puis est croissante de 5 à l'infini
(dérivée = 2r -10)
donc f(r) > 0 
r > 16,2 R1 > r
T'as pas fait une erreur de signe là ?:
10r = (r-10)(r+10)
10r = r² + 10²
r² - 10r - 100 = 0
C'est pas plutôt 10r = r² - 10²
et donc -r² + 10r + 100 = 0
???
Bonjour,
erreur de frappe uniquement sur cette ligne, le reste est bon:
10r = r2 - 102
pour R1 > r il faut que R1 - r > 0
R1 - r =
comme le dénominateur est toujours positif, il faut que le numérateur soit positif
100 + 10r - r2 > 0
r2 - 10r - 100 < 0
Désolé Daniel, j'ai mi un peu de temps avant de répondre,
Merci pour la question a), j'l'ai refais c'est bon j'ai pigé, mais par contre j'comprends toujours pas la question b), donc si tu pouvais m'expliquer comment tu fais stp...
Bonjour,
est-tu d'accord avec le message du 02/11/08 à 19:03 ?
R1 - r > 0 r2 - 10r - 100 < 0
if faut étudier le signe de r2 - 10r - 100
admet 2 racines r1 et r2 avec r1=5-55 et r2=5+55
r2 - 10r - 100 = (r-r1)(r-r2)
(r-r1)
négatif de -
à r1
s'annule pour r1
positif de r1 à +
(r-r2)
négatif de - à r2
s'annule pour r2
positif de r2 à +
(r-r1)(r+r2)
positif de - à r1
s'annule pour r1
négatif de r1 à r2
s'annule pour r2
positif de r2 à +
la seule solution est de r1 à r2
comme r ne peut être que positif donc de 0 à r2
R1 - r > 0 r2 - 10r - 100 < 0 r 
[0,r2[ r < r2 = 5+55
Annuler
connectez vous