Inscription / Connexion Nouveau Sujet
différences entre représentation de forces
Bnojour à tous, j'ai un exo sur la suspension d'un feu de signalisation immobile soumis à son poids P et à deux forces de tension T1 et T2 exercées par 2 cables
On me demande de retrouver par graphique T1 et T2, j'ai fait le dessin avec le poids P valant 48 kg soit 470N et pour trouver T1 et T2, j'ai fait un angle de 70° comme dans l'énoncé ( 70° pour chaque cable par rapport à la droite du poids P, donc 70 + 70 ) et je me suis arrangé pour que T1=T2 et que T1 +T2 + P = O
Je trouve 680N pour chaque fil.
Ensuite on me demande de retrouver T1 et T2 par projection sur 2 axes orthogonaux, je ne comprends pas trop quelle elle est la différence entre les 2 manières.
Merci de me répondre au plus vite !
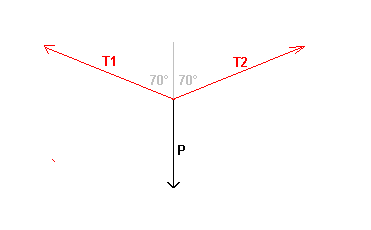
Projection sur un axe horizontal:
T2.sin(70°) - T1.sin(70°) = 0 --> T1 = T2
Projection sur un axe vertical:
P - T1.cos(70°) - T2.cos(70°) = 0
48*9,8 - 2T1.cos(70°) = 0
T1 = T2 = 470,4/(2*cos(70°)) = 688 N
-----
Sauf distraction. 
merci mais je ne comprends pas très bien ... surtout sur l'axe vertical, pouvez vous m'expliquer s'il vous plait ?
On choisit un axe vertical quelconque et on lui donne un sens positif (celui qu'on veut, mais on ne peut pas le changer en cours de route)
Ici, j'ai choisi l'axe en bleu avec le sens positif vers le bas.
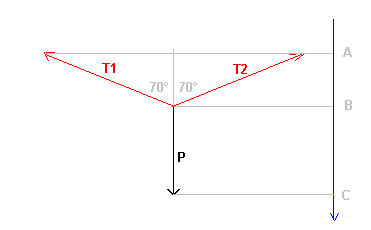
Si on projette orthogonalement P sur l'axe en bleu, on obtient le vecteur BC
BC a la même norme que P et il est dirigé dans le sens positif de l'axe.
On a donc que la projection de P sur l'axe a la même mesure que P.
Si on projette orthogonalement T2 sur l'axe en bleu, on obtient le vecteur BA
BA "mesure" T2*cos(70°) et il est dirigé dans le sens négatif de l'axe.
On a donc que la projection de T2 sur l'axe a la même mesure que -T2.cos(70°)
Si on projette orthogonalement T1 sur l'axe en bleu, on obtient aussi le vecteur BA
BA "mesure" T1*cos(70°) et il est dirigé dans le sens négatif de l'axe.
On a donc que la projection de T1 sur l'axe a la même mesure que -T1.cos(70°)
Comme le système est en équilibre, la projection des forces sur un axe quelconque est = 0
Donc c'est vrai aussi pour l'axe en bleu.
On a donc P - T2.cos(70°) - T1.cos(70°) = 0
Ceci permet d'avoir une équation liant les inconnues T1 et T2
Pour pouvor déterminer ces inconnues, on a besoin d'une seconde équation.
On trouve cette seconde équation en projetant les 3 forces sur un axe quelconque mais qui ne peut plus être vertical (il doit avoir une autre direction que l'axe qui a déjà servi)
Pour la facilité, on choisit cette fois un axe horizontal de sens positif vers la droite (ou peut prendre l'autre sens si on veut mais pas changer en cours de route).
La projection de P sur cet axe est 0 (puisque P et l'axe horizontal sont perpendiculaires)
La projection de T2 sur cet axe est T2.sin(70°)
La projection de T1 sur cet axe est -T1.sin(70°)
Comme le système est en équilibre, la projection des forces sur un axe quelconque est = 0
Donc c'est vrai aussi pour l'axe horizontal choisi.
--> on obtient l'équation:
T2.sin(70°) - T1.sin(70°) = 0
On a donc un système de 2 équations à 2 inconnues (T1 et T2), car P est une donnée.
P - T2.cos(70°) - T1.cos(70°) = 0
T2.sin(70°) - T1.sin(70°) = 0
La résolution du système permet de calculer les valeurs de T1 et de T2.
-----
Compris ?



